Главная
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
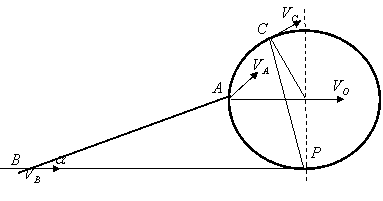
13.1. Колесо радиусом R перекатывается без
скольжения по горизонтальной прямой MN, скорость центра V0 постоянна. В точке А к колесу шарнирно прикреплен стержень
АВ длиной l, конец В которого скользит слева от
колеса по прямой MN.
Определить угловую скорость стержня, скорость его концов А и В, а также
скорость точки С колеса в положении, когда радиус ОА колеса составляет с
вертикалью угол φ.
Дано: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти: ![]() , VA, VB, VC.
, VA, VB, VC.
Решение: Мгновенный центр скоростей колеса в точке Р – соприкосновение колеса с прямой. Тогда угловая скорость:
![]() .
.
Из рисунка видно, что:
![]() ,
,
![]() ,
,
![]() .
.
Скорость точки А колеса:
![]() ,
,
Скорость точки С колеса:
![]() .
.
Проецируем скорости на стержень АВ:
![]() .
.
13.2. Колесо радиусом R перекатывается
без скольжения по горизонтальной прямой MN, скорость
центра V0 постоянна. В точке А к
колесу шарнирно прикреплен стержень АВ длиной l, конец В
которого скользит слева от колеса по прямой MN.
Определить угловую скорость стержня, скорость его концов А и В, а также
скорость точки С колеса в положении, когда радиус ОА колеса составляет с
вертикалью угол φ.
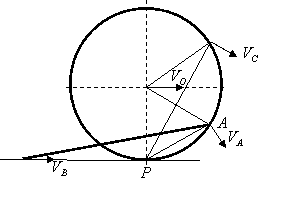 Дано:
Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() , VA, VB, VC.
, VA, VB, VC.
Решение: Мгновенный центр скоростей колеса в точке Р – соприкосновение колеса с прямой. Тогда угловая скорость:
![]() .
.
Из рисунка видно, что ![]() равносторонний,
поэтому
равносторонний,
поэтому ![]() , сторона
, сторона ![]() по теореме косинусов:
по теореме косинусов:
![]()
Скорость точки А колеса:
![]() ,
,
Скорость точки С колеса ![]() .
.
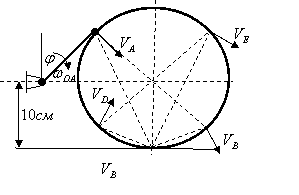
13.3. Стержень ОА
длиной 10см вращается вокруг оси О с постоянной угловой скоростью ![]() ; при этом он поворачивает и передвигает цилиндр радиусом
10см, лежащий на горизонтальной плоскости и соединенный со стержнем шарниром А.
Ось цилиндра С всегда остается параллельной оси О вращения стержня ОА.
; при этом он поворачивает и передвигает цилиндр радиусом
10см, лежащий на горизонтальной плоскости и соединенный со стержнем шарниром А.
Ось цилиндра С всегда остается параллельной оси О вращения стержня ОА.
Определить скорости концов двух взаимно перпендикулярных диаметров АВ и
DE цилиндра, а также его угловую скорость
в момент времени, когда стержень ОА составляет с вертикалью угол ![]() .
.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() , VA, VB, VC.
, VA, VB, VC.
Решение: Скорость точки А стержня ОА:
![]() .
.
Мгновенный центр скоростей колеса в точке Р – соприкосновение колеса с прямой. Тогда угловая скорость:
![]() .
.
Из рисунка видно, что ![]() равносторонний,
поэтому
равносторонний,
поэтому ![]() , сторона
, сторона ![]() по теореме косинусов:
по теореме косинусов:
![]()
Скорость точки А колеса:
![]() ,
,
Скорость точки С колеса ![]() .
.
13.4. Линейка эллипсографа ВС приводится в движение кривошипом ОА,
вращающимся с постоянной угловой скоростью ![]() вокруг оси О. К
линейке жестко прикреплена прямоугольная пластинка BCDE.
вокруг оси О. К
линейке жестко прикреплена прямоугольная пластинка BCDE. ![]() .
.
Определить скорости точек B,C, D и E в момент времени, когда кривошип ОА
составляет с горизонталью угол ![]() .
.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение: Расставим на расчетной схеме все скорости точек. Скорости точки А:
![]() .
.

Из расчетной схемы видно, что:
![]() ,
,
![]() .
.
![]() так как
так как ![]() и тогда
и тогда
![]() .
.
![]() .
.
Мгновенный центр скоростей в точке Р (точке пересечения перпендикуляров к скоростям). Угловая скорость этого центра:
![]() .
.
Тогда скорости точек:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
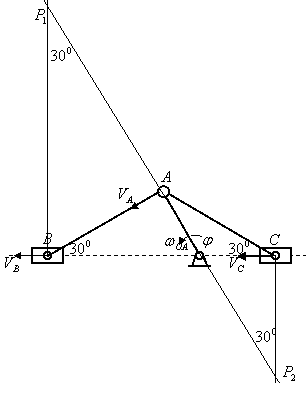
14.1. Кривошип ОА кривошипно-шатунного механизма ОАВ вращается с
постоянной угловой скоростью ![]() ,
,
![]() .
К шарниру А прикреплен второй шатун АС, конец С которого скользит по прямой
ВОС.
.
К шарниру А прикреплен второй шатун АС, конец С которого скользит по прямой
ВОС.
Определить в положение, указанном на чертеже, скорости В и С и угловые
скорости шатунов ![]() и
и ![]() .
.
 Дано:
Дано: ![]() ,
,
![]() ,
,
![]() .
.
Найти: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение: Изобразим механизм в заданном положении. Изобразим направление скоростей всех точек.
Определим скорость точки А:
![]() .
.
Проецируем скорости на стержень АВ:
![]() ,
,
Откуда скорость точки В:
![]() .
.
Проецируем скорости на стержень АВ:
![]() ,
,
Откуда скорость точки В:
![]() .
.
Обозначим мгновенные центры
скоростей для стержней АВ и АС в точках ![]() и
и ![]() соответственно. Из рисунка:
соответственно. Из рисунка:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Угловые скорости стержней:
![]() и
и
![]() .
.
14.2. Шатун АВ кривошипно-шатунного механизма ОАВ связан шарнирно со
стержнем CD, а последний – со стержнем DE, который может вращаться вокруг точки Е.
Определить скорость шарниров С и D, а также угловые
скорости звеньев CD и DE в положении механизма, указанном на чертеже, если угловая
скорость кривошипа ОА постоянна и равна ![]() .
.
![]() ;
;
![]() .
Остальные размеры даны в таблице.
.
Остальные размеры даны в таблице.
Дано: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
 Решение: Скорость точки А:
Решение: Скорость точки А:
![]() .
.
Спроектировав скорости ![]() и
и ![]() на шатун АВ:
на шатун АВ:
![]() .
.
Спроектировав скорости ![]() и
и ![]() на стержень CD:
на стержень CD:
![]() .
.
Как видно из рисунка, мгновенный центр скоростей стержня CD в точке Е и угловая скорость тогда:
![]() .
.
14.3. Шатун АВ кривошипно-шатунного механизма ОАВ связан шарнирно со
стержнем CD, а последний – со стержнем DE, который может вращаться вокруг точки Е.
Определить скорость шарниров С и D, а также
угловые скорости звеньев CD и DE в положении механизма, указанном на чертеже, если угловая
скорость кривошипа ОА постоянна и равна ![]() .
. ![]() ;
; ![]() . Остальные размеры даны в таблице.
. Остальные размеры даны в таблице.
Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
 Найти:
Найти: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение: Скорость точки А:
![]() .
.
Спроектировав скорости ![]() и
и ![]() на шатун АВ:
на шатун АВ:
![]() .
.
Спроектировав скорости ![]() и
и ![]() на стержень CD:
на стержень CD:
![]() .
.
Как видно из рисунка, мгновенный центр скоростей стержня CD в точке P, и угловая скорость тогда:
![]() .
.
И угловая скорость стержня DE:
![]() .
.
14.4. Кривошип ОА длиной 10см вращается с постоянной угловой скоростью ![]() с помощью стержня АВ
приводит в движение систему рычагов ВС, BD и DE длиной
40см каждый.
с помощью стержня АВ
приводит в движение систему рычагов ВС, BD и DE длиной
40см каждый.
Определить угловые скорости звеньев АВ, ВС, BD и DE в положении механизма, указанном на чертеже.
Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение: Изобразим систему в заданном положении и расставим скорости точек.
Скорость точки А:
![]() .
.
Из расчетной схемы видно, что:
![]()
![]() .
.

![]()
![]() .
.
Проекции скоростей на стержень OAB:
![]() .
.
Проекции скоростей на стержень OAB:

![]() .
.
Угловая скорость стержня ВС:
![]() .
.
Угловая скорость стержня DB:
![]() ,
,
Угловая скорость стержня DB:
![]() .
.
14.5. Кривошип ОА длиной 10см вращается с постоянной угловой скоростью ![]() с помощью стержня
с помощью стержня ![]() приводит в движение
систему рычагов
приводит в движение
систему рычагов ![]() ,
, ![]() и
и ![]() длиной 40см каждый.
длиной 40см каждый.
Определить угловые скорости звеньев ![]() ,
, ![]() ,
, ![]() и
и ![]() в положении механизма,
указанном на чертеже.
в положении механизма,
указанном на чертеже.
Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение: Скорость точки А:
![]() .
.
Из расчетной схемы видно, что:
![]() .
.
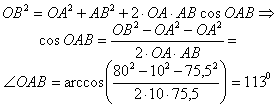
![]()

![]() .
.
Проекции скоростей на стержень OAB:
![]() .
.
Проекции скоростей на стержень OAB:
![]() .
.
Угловая скорость стержня ВС:
![]() .
.
Угловая скорость стержня DB:
![]() ,
,
Угловая скорость стержня DB:
![]() .
.
14.6. Кривошип ОА длиной 30см вращается вокруг оси О с угловой
скоростью ![]() . Зубчатое колесо 2 радиусом 20см катится без скольжения по
неподвижному колесу 1 и приводит в движение связанный с ним шатун ВС длиной l.
. Зубчатое колесо 2 радиусом 20см катится без скольжения по
неподвижному колесу 1 и приводит в движение связанный с ним шатун ВС длиной l.
Определить угловую скорость шатуна ВС и скорость точки С в положение
механизма, когда кривошип ОА и радиус АВ образуют с горизонталью углы ![]() и
и ![]() .
.
Дано: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() .
.
Решение: Скорость точки А:

![]() .
.
Мгновенный центр скоростей колеса 2 в точке Р на стыке колес 1 и 2. Угловая скорость этого МЦС:
![]() .
.
Из схемы видно, что:
![]() .
.
Скорость точки В:
![]() .
.
Мгновенный центр скоростей
стержня ВС в точке ![]() . С угловой скоростью
. С угловой скоростью ![]() , а расстояние
, а расстояние ![]() .
.
Тогда скорость точки С:
![]() .
.
15.1. Равносторонний треугольник со стороной 1м движется в плоскости
чертежа.
Определить ускорения точек А и В, если ускорение точки О ![]() , угловая скорость
, угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
 Найти:
Найти: ![]() ,
, ![]() .
.
Решение: Тангенциальные и нормальные ускорения точек:
![]() и
и
![]() .
.
Общие ускорения точек А и В:
![]() и
и
![]() .
.
И в скалярном виде:
![]() ,
,
![]()
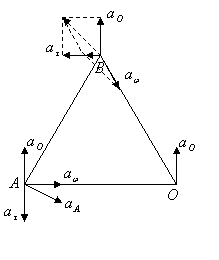
15.2. Квадрат со стороной 2м движется в плоскости чертежа так, что
ускорение точки О ![]() , угловая скорость
, угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Найти ускорение вершин А и В квадрата.
 Дано:
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() .
.
Решение: Тангенциальные и нормальные ускорения точек А и В соответственно:
![]() и
и ![]()
![]() и
и ![]() .
.
Общие ускорения точек А и В:
![]() и
и
![]() .
.
И в скалярном виде:
![]() ,
,
![]()
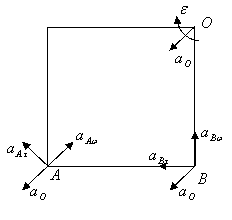
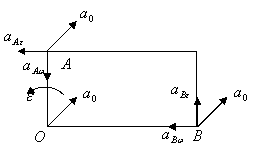
15.3. Квадрат со стороной 2м движется в плоскости чертежа так, что
ускорение точки О ![]() , угловая скорость
, угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Найти ускорение вершин А и В квадрата.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() .
.
Решение: Из рисунка видно, что:
![]() .
.
Осестремительные ускорения точек А и В соответственно:
![]() и
и
![]() .
.
Касательные ускорения точек А и В соответственно:
![]() и
и
![]() .
.
Из рисунка видно, что:
![]() .
.
![]() .
.
Абсолютное ускорение точек А и В соответственно:
![]() и
и
![]() ,
,
А в скалярном виде:
![]() .
.
![]() .
.
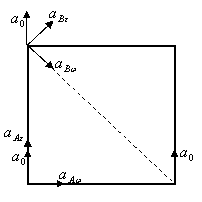
15.4. Квадрат со стороной 2м движется в плоскости чертежа так, что
ускорение точки О ![]() , угловая скорость
, угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Найти ускорение вершин А и В квадрата.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() .
.
Решение: Из рисунка видно, что:
![]() .
.
Осестремительные ускорения точек А и В соответственно:
![]() и
и
![]() .
.
Касательные ускорения точек А и В соответственно:
![]() и
и
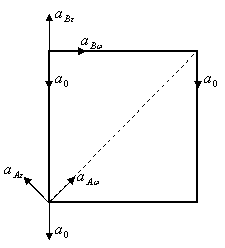
![]() .
.
Из рисунка видно, что:
![]() .
.
![]() .
.
Абсолютное ускорение точек А и В соответственно:
![]() и
и
![]() ,
,
А в скалярном виде:
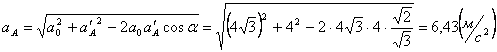 .
.
![]() .
.
15.5. Прямоугольная пластина размером ![]() движется в плоскости
чертежа так, что ускорение точки О
движется в плоскости
чертежа так, что ускорение точки О ![]() , угловая скорость
, угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() .
.
Найти ускорение вершин А и В пластинки.
Дано: ![]() ,
, ![]() ,
, ![]() .
.
Найти: ![]() ,
, ![]() .
.
Решение: Осестремительные ускорения точек А и В:
![]() и
и
![]() .
.
Касательные ускорения точек А и В:
![]() ,
,
![]() .
.
Абсолютное ускорение точек А и В:
![]() и
и
![]() .
.
 Из
схемы видно, что:
Из
схемы видно, что:
![]() и
и
![]() .
.
![]() и тогда:
и тогда:
![]() и
и
![]() .
.
15.6. Найти для заданного положения
механизма скорости и ускорения точек B и C, а также угловую скорость и угловое ускорение звена,
которому эти точки принадлежат.
Дано: Cхема
механизма в заданном положении (рис.1), исходные данные таковы, что OA =
Найти: ![]() .
.
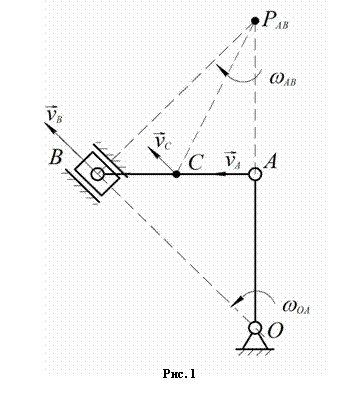
Решение: 1) Определение скорости точек и угловой скорости звена AB: вычисляем модуль скорости точки A при заданном положении механизма:
![]() .
.
Скорость точки А перпендикулярна кривошипу ОА. Скорость ползуна В направлена вдоль ОВ. Мгновенный центр скоростей PAB шатуна АВ находится в точке пересечения перпендикуляров, проведенных из точек A и B к их скоростям.
Угловая скорость звена AB:
![]() .
.
Расстояния АРАВ, ВРАВ
и СРАВ определяются
из рассмотрения треугольников АСРАВ
и АВРАВ :
APАВ=OA=40 см, ВPАВ=![]() см, СPАВ=
см, СPАВ=![]() см.
см.
В соответствии с этим ![]() ,
, ![]() ;
; ![]() ;
; ![]() .
.
Вектор ![]() направлен
перпендикулярно отрезку СРАВ в сторону, соответствующую направлению
вращения звена АВ.
направлен
перпендикулярно отрезку СРАВ в сторону, соответствующую направлению
вращения звена АВ.
2) Определение ускорений точек и углового ускорения звена AB (рис. 2).
Ускорение точки A складывается из вращательного и центростремительного ускорений:
![]() ,
,
где ![]() ,
, ![]() .
.
Согласно теореме об ускорениях точек плоской фигуры:
![]()
или ![]() . (1)
. (1)
Вектор ![]() направлен от A к
направлен от A к 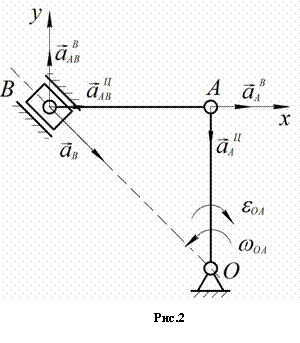 О. Вектор
О. Вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() и направлен в сторону,
противоположную
и направлен в сторону,
противоположную ![]() , (т.к. из условия задачи движение кривошипа OA замедленное).
, (т.к. из условия задачи движение кривошипа OA замедленное).
Центростремительное ускорение
точки B во вращательном движении шатуна AB вокруг полюса A: ![]() и направлено от B к
A.
и направлено от B к
A.
Ускорение ![]() направлено вдоль линии
OB, а
направлено вдоль линии
OB, а ![]() . Зададим произвольно их направления:
. Зададим произвольно их направления: ![]() -
вертикально вверх,
-
вертикально вверх, ![]() - от B к O. Эти
ускорения определим из уравнений проекций векторного равенства (2) на оси
координат. Знак в ответе показывает, соответствует ли истинное направление
вектора принятому при расчете.
- от B к O. Эти
ускорения определим из уравнений проекций векторного равенства (2) на оси
координат. Знак в ответе показывает, соответствует ли истинное направление
вектора принятому при расчете.
Выбрав направление осей x и y, как показано на рис.2, получаем:
![]() , (2)
, (2)
![]() . (3)
. (3)
Из уравнения (2) находим
![]() .
.
Из уравнения (3) получаем
![]() .
.
Следовательно, ускорение ![]() направлено так, как показано на рисунке, а
направлено так, как показано на рисунке, а ![]() – в противоположную
сторону. Истинная картина ускорений для точки B показана на рис.3.
– в противоположную
сторону. Истинная картина ускорений для точки B показана на рис.3.
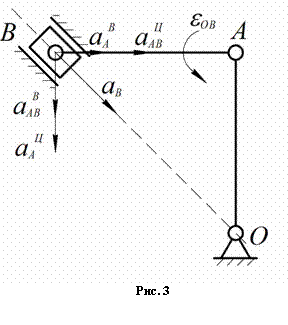
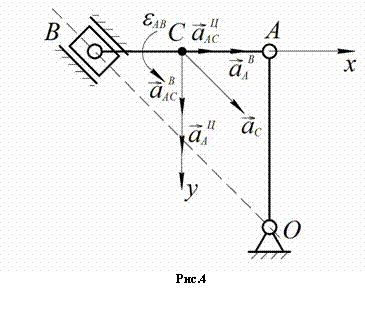
Угловое ускорение шатуна AB:
![]() .
.
Направление ![]() относительно полюса A определяет направление углового
ускорения
относительно полюса A определяет направление углового
ускорения ![]() . В данном случае,
. В данном случае, ![]() не совпадает с
направлением
не совпадает с
направлением ![]() , следовательно, движение звена замедленное.
, следовательно, движение звена замедленное.
Определим ускорение точки C:
![]() .
.
Вращательное и центростремительное ускорения точки C во вращательном движении AB вокруг полюса A:
![]() ;
;
![]() .
.
Вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() и направлен
соответственно угловому ускорению
и направлен
соответственно угловому ускорению ![]() .
.
Ускорение ![]() находим методом
проекций (рис.4):
находим методом
проекций (рис.4):
![]() ,
, ![]() ,
,
![]() .
.
В результате вычислений получаем:
![]() ,
,
![]() ,
,
![]()
15.7. Механизм состоит из стержней 1, 2, 3, и ползунов В и Е, соединенных друг с другом и с неподвижной опорой О1 (рис. 1).
Дано: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; VВ = 8
м/с; аВ =10 м/с2; l1=0,4
м; l2=1,2 м; l3 =1,4 м, AD = DB.
; VВ = 8
м/с; аВ =10 м/с2; l1=0,4
м; l2=1,2 м; l3 =1,4 м, AD = DB.
Определить: VD, VЕ, ![]() , aА,
, aА,![]() .
.
Указания.
Задача - на исследование плоскопараллельного движения твердого тела. При ее
решении для определения скоростей точек механизма и угловых скоростей его
звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и
понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие)
к каждому звену механизма в отдельности. При определении ускорений точек
механизма исходить из векторного равенства
![]() , где А – точка, ускорение
, где А – точка, ускорение ![]() которой или
задано, или непосредственно определяется по условиям задачи (если точка А
движется по дуге окружности, то
которой или
задано, или непосредственно определяется по условиям задачи (если точка А
движется по дуге окружности, то ![]() ); В – точка, ускорение
); В – точка, ускорение ![]() которой нужно
определить.
которой нужно
определить.
Решение.
1. Строим положение механизма в соответствии с заданными углами (рис. 1).
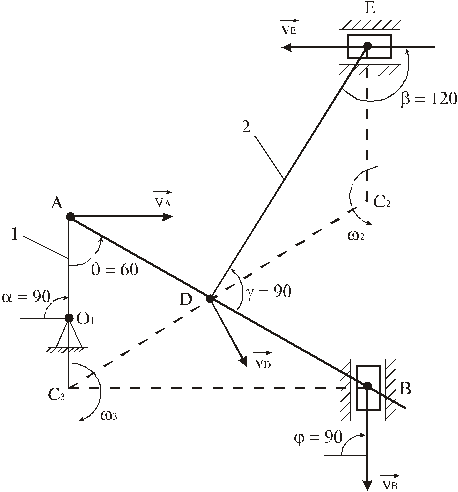
2. Определяем VD. Точка D принадлежит стержню АВ. Для
определения VD сначала
найдем величину и направление скорости ![]() точки А.
точки А. ![]() ^О1А.
Теперь, зная
^О1А.
Теперь, зная ![]() и направление
и направление ![]() , воспользуемся теоремой о проекциях скоростей двух точек
тела на прямую, соединяющую эти точки.
, воспользуемся теоремой о проекциях скоростей двух точек
тела на прямую, соединяющую эти точки.
Учитывая, что проекции скоростей должны иметь одинаковые знаки,
устанавливаем в какую сторону направлен вектор ![]() :
:
VВcos600 = VAcos300;
VA=VВcos300/cos600=13,86 м/с.
Зная ![]() и
и ![]() , строим мгновенный центр скоростей (МЦС) стержня АВ, это
точка С3, лежащая на пересечении перпендикуляров к
, строим мгновенный центр скоростей (МЦС) стержня АВ, это
точка С3, лежащая на пересечении перпендикуляров к ![]() и
и![]() , восстановленных из точек А и В.
, восстановленных из точек А и В.
По направлению вектора ![]() определяем направление
поворота стержня АВ вокруг МЦС С3. Вектор скорости
определяем направление
поворота стержня АВ вокруг МЦС С3. Вектор скорости ![]() перпендикулярен
отрезку С3D,
соединяющему точки D и
С3, и направлен в сторону поворота. Величину VD найдем
из пропорции: VD/С3D =VA/С3А.
Треугольник АО3D
– равносторонний. С3D
= С3А =0,7 м; VD =VA =13,86 м/с.
перпендикулярен
отрезку С3D,
соединяющему точки D и
С3, и направлен в сторону поворота. Величину VD найдем
из пропорции: VD/С3D =VA/С3А.
Треугольник АО3D
– равносторонний. С3D
= С3А =0,7 м; VD =VA =13,86 м/с.
3.
определяем ![]() . Точка Е принадлежит стержню ЕD. Направление
. Точка Е принадлежит стержню ЕD. Направление ![]() найдем, учитывая, что
точка Е принадлежит одновременно ползуну, движущемуся вдоль направляющих
поступательно:
найдем, учитывая, что
точка Е принадлежит одновременно ползуну, движущемуся вдоль направляющих
поступательно:
VDcos600 = VЕcos600;
VЕ =VD =13,86 м/с.
4. Определяем ![]() . Строим МЦС стержня (т. С2).
. Строим МЦС стержня (т. С2). ![]() dc2E – равнобедренный, c2d = c2E; c2d определим по теореме синусов:
dc2E – равнобедренный, c2d = c2E; c2d определим по теореме синусов:
c2d/sin300 = dE/ sin1200,
c2d = l2
sin300 /sin1200 = l2
sin300/ cos300 =0,69 м, тогда
![]() =VD/ c2d =20 с-1.
=VD/ c2d =20 с-1.
5. Определяем аА.
Изображаем все векторы ускорений (рис. 2).
Точка А движется по окружности радиуса О1А, в этом случае ![]() представлена двумя
составляющими:
представлена двумя
составляющими:
![]() .
.
вектор ![]() направлен вдоль АО1,
а
направлен вдоль АО1,
а ![]() – перпендикулярно АО1,
где:
– перпендикулярно АО1,
где:
VA=![]() ;
;
![]() = VA/ l1 =34,65 с-1,
= VA/ l1 =34,65 с-1,
![]() =480 м/с2.
=480 м/с2.
Для определения ![]() воспользуемся равенством:
воспользуемся равенством:
![]() .
.
Вектор ![]() направлен вдоль ВА,
вектор
направлен вдоль ВА,
вектор ![]() перпендикулярен ВА.
перпендикулярен ВА.
Численно
![]() .
.
Находим ![]() с помощью построенного
МЦС С3 стержня 3:
с помощью построенного
МЦС С3 стержня 3:
![]() ,
,
![]() м/с2.
м/с2.
Таким образом, у величин, входящих в равенство, неизвестны только
числовые значения ![]() и
и ![]() . Их можно найти, спроецировав обе части равенства на
какие-нибудь две оси.
. Их можно найти, спроецировав обе части равенства на
какие-нибудь две оси.
Чтобы определить ![]() , спроецируем обе части равенства на ось у:
, спроецируем обе части равенства на ось у:
![]() ,
,
![]() м/с2.
м/с2.
Так как ![]() , то, следовательно, вектор
, то, следовательно, вектор ![]() направлен в
противоположную сторону от показанного.
направлен в
противоположную сторону от показанного.
Чтобы определить ![]() , спроектируем обе части равенства на ось х:
, спроектируем обе части равенства на ось х:
![]() ,
,
![]() м/с2.
м/с2.
![]() < 0, следовательно, вектор
< 0, следовательно, вектор ![]() направлен в
противоположную сторону:
направлен в
противоположную сторону:
![]() м/с2.
м/с2.
Определяем ![]() из равенства
из равенства ![]() :
:
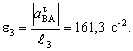
Ответ: VD= 13,86 м/с, VE =13,86 м/с, ![]() = 20 c-1, aA = 601,4 м/с2,
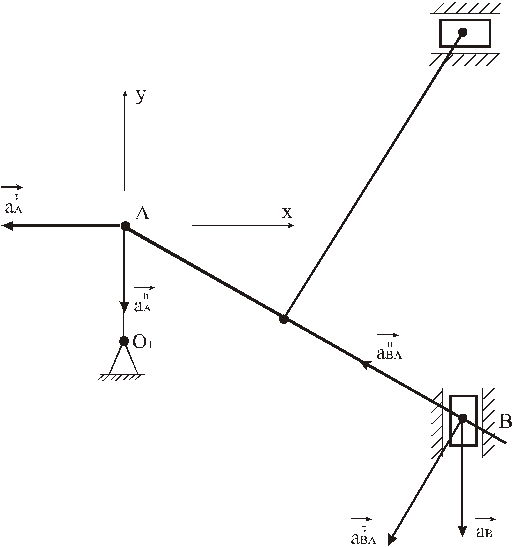
= 20 c-1, aA = 601,4 м/с2, ![]() =161,3 с-2.
=161,3 с-2.
15.8. Механизм, см. рис.1,
состоит из стержней 1, 2, 3, 4 и ползуна Е,
соединенных между собой и с неподвижными опорами О1 и О2
шарнирами.
Дано: ![]() =0,
=0, ![]() =600,
=600, ![]() =300,
=300, ![]() =0,
=0,
![]() =1200,
=1200,
![]() =6с-1,
=6с-1,
![]() =10с-2,
=10с-2,
![]() =0.4
м,
=0.4
м, ![]() =1.2 м,
=1.2 м, ![]() =1.6 м,
=1.6 м, ![]() =0.6 м.
=0.6 м.
Определить: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и положение мгновенных
центров скоростей звеньев, если дано:
и положение мгновенных
центров скоростей звеньев, если дано:
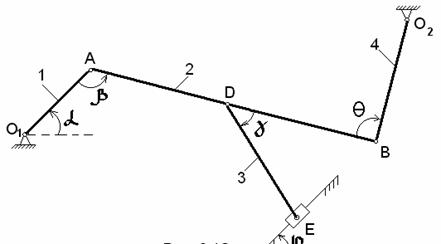
Рис.1
Решение. Согласно условию задачи
вычерчиваем механизм в заданном положении (рис.1). Исходя из направления ![]() , находим направления скоростей точек А, В, Е (показано на рис. 2). Восстанавливаем перпендикуляры к
скоростям
, находим направления скоростей точек А, В, Е (показано на рис. 2). Восстанавливаем перпендикуляры к
скоростям ![]() и
и ![]() в точках А и В
находим положение мгновенного центра скоростей звена АВ – точка Р2.
Соединив точку D с Р2 и восстановив
перпендикуляр к Р2D в точке D, находим направление
скорости
в точках А и В
находим положение мгновенного центра скоростей звена АВ – точка Р2.
Соединив точку D с Р2 и восстановив
перпендикуляр к Р2D в точке D, находим направление
скорости ![]() . В точке пересечения перпендикуляров к скоростям
. В точке пересечения перпендикуляров к скоростям ![]() и
и ![]() находится мгновенный
центр скоростей звена DE – точка Р3. Находим теперь линейные
скорости точек А, В, D, Е и угловые
скорости звеньев
находится мгновенный
центр скоростей звена DE – точка Р3. Находим теперь линейные
скорости точек А, В, D, Е и угловые
скорости звеньев ![]() ,
, ![]() ,
, ![]() .
.
Имеем ![]() м/с.
м/с.
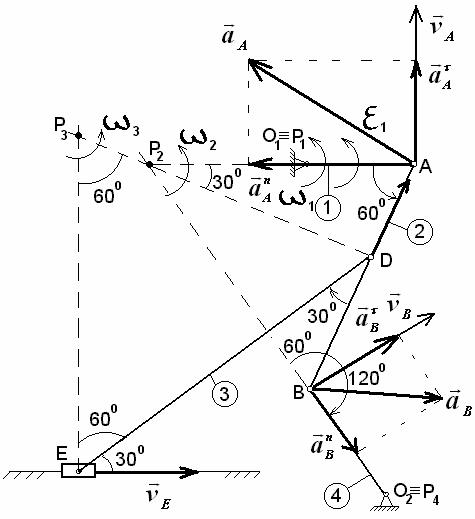
Рис.2
Так как точка А принадлежит и звену 2, то
![]()
Из равностороннего треугольника АР2В следует, что АР2=ВР2=АВ, следовательно АР2=ВР2=l2=1.2 м.
Тогда ![]() с-1.
с-1.
Значит ![]() м/с,
м/с,
![]() м/с.
м/с.
Однако точка В принадлежит и звену ВО2, поэтому
![]() ,
,
откуда ![]() с-1.
с-1.
Точка D принадлежит также звену DE, поэтому
![]()
Из равностороннего треугольника DP3E следует, что
DP3=EP3=DE=l3=1.6 м.
Следовательно ![]() с-1,
поэтому линейная скорость точки Е
будет
с-1,
поэтому линейная скорость точки Е
будет ![]() м/с.
м/с.
Найдем
ускорения точек А и В и угловое ускорение звена АВ. Учитывая, что ускорение точки А равно ![]()
Где ![]() м/с2,
м/с2,
![]() м/с2,
м/с2,
значит ![]() м/с2.
м/с2.
Для определения ускорения точки В используем закон распределения ускорений.
![]() ,
,
или ![]() ,
,
где ![]() ,
направлено перпендикулярно к О2В,
,
направлено перпендикулярно к О2В,
![]() м/с2, направлено от В к О2,
м/с2, направлено от В к О2,
![]() м/с2, направлено перпендикулярно к О1А,
м/с2, направлено перпендикулярно к О1А,
![]() м/с2, направлено от А к О1,
м/с2, направлено от А к О1, ![]() , направлено перпендикулярно к АВ,
, направлено перпендикулярно к АВ,
![]() м/с2,
направлено от В к А.
м/с2,
направлено от В к А.
Направление векторов показано на рис. 3.
Используя
метод проекций находим ![]() ,
,
Откуда
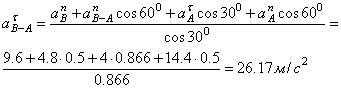
Значит
![]() с-2.
с-2.
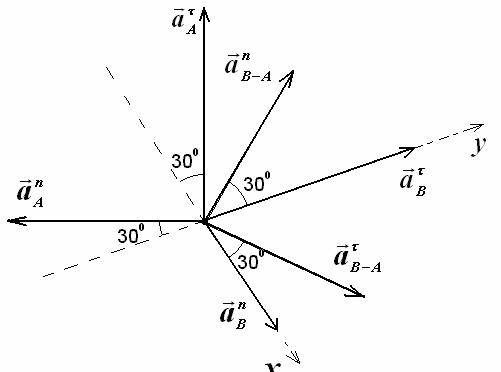
Рис.3
Проецируя на ось «У» определяем
![]()
![]() м/с2
м/с2
Тогда полное ускорение точки В определяется
![]() м/с2
м/с2
Ответ: ![]() м/с;
м/с; ![]() м/с;
м/с; ![]() м/с;
м/с; ![]() м/с;
м/с; ![]() с-1;
с-1; ![]() с-1;
с-1; ![]() с-1;
с-1; ![]() м/с2;
м/с2; ![]() м/с2;
м/с2; ![]() с-2.
с-2.
15.9. Колесо катится без
скольжения по неподвижной прямой поверхности. Скорость точки O постоянна и равна 100 см/с (см. рис.
а).
Определить: угловую скорость колеса, скорости точек A, B, C и ускорения точек A, C, P, если R = 50 см, r = 40 см.
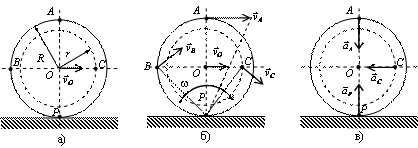
Решение. Колесо совершает плоскопараллельное движение. Качение происходит без скольжения, следовательно, в данном случае точка касания колеса с неподвижной поверхностью – точка P – является МЦС. Определим угловую скорость колеса согласно формуле
![]()
Зная расстояния от точек A, B и C до МЦС, можно найти их скорости по формуле
![]()
![]()
![]()
Векторы скоростей точек колеса направлены перпендикулярно отрезкам, соединяющим их с МЦС (см. рис. б). В соответствии с теоремой о проекциях скоростей двух точек тела на прямую, соединяющую эти точки, убеждаемся в правильности полученных результатов.
Перейдем к определению ускорений. В качестве полюса выбираем точку O. Ускорение полюса равно нулю, так как эта точка движется равномерно и прямолинейно. Поэтому ускорения точек будут равны их ускорениям во вращательном движении вокруг полюса. Например, для точки А
![]() .
.
Дифференцируя
по времени выражение ![]() и учитывая, что OP = const и
и учитывая, что OP = const и ![]() = const, получим
= const, получим ![]() Таким образом,
ускорения всех точек, включая МЦС, состоят из осестремительных ускорений во
вращении вокруг полюса О
Таким образом,
ускорения всех точек, включая МЦС, состоят из осестремительных ускорений во
вращении вокруг полюса О
![]()
![]() ;
;
![]()
и направлены от соответствующих точек к полюсу (см. рис. в).
15.10. Кривошип ОА
кривошипно-ползунного механизма, приведенного на рис., вращается вокруг
неподвижной оси с угловой скоростью ![]() и угловым ускорением
и угловым ускорением ![]() . Положение механизма определяется углом
. Положение механизма определяется углом ![]() .
.
Определить: угловую скорость и угловое ускорение шатуна АВ, а также скорость и ускорение ползуна B, если длина кривошипа ОА = 10 см, а длина шатуна АВ = 30 см.
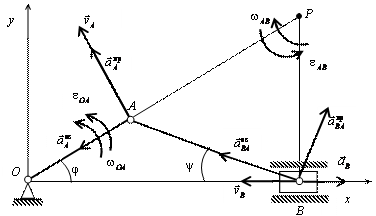
Решение. Вначале определим скорость точки А кривошипа
![]()
Затем, зная
направления скоростей точек А и В, найдем положение МЦС на пересечении
перпендикуляров к скоростям этих точек – точку P. Для определения угловой скорости шатуна ![]() и скорости точки В находим длины отрезков, соединяющих
точки А и В с МЦС. Из теоремы синусов следует, что
и скорости точки В находим длины отрезков, соединяющих
точки А и В с МЦС. Из теоремы синусов следует, что
![]()
Вычислим длины отрезков:
![]()
![]()
![]() .
.
Теперь найдем искомые
величины:
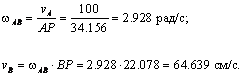
Определим
ускорение точки В и угловое ускорение
шатуна АВ. Здесь надо иметь в виду,
что расстояние от точки А до МЦС не является
постоянным и зависит от положения механизма, т.е. от времени. Поэтому
продифференцировать по времени угловую скорость шатуна не представляется
возможным. Поступим следующим образом. Для нахождения ускорения точки В воспользуемся векторным равенством
![]()
и спроецируем его на оси
координат xOy (см. рис. ). При этом учтем, что вектор ![]() лежит на прямой ОВ, так как точка В движется прямолинейно, вектор
лежит на прямой ОВ, так как точка В движется прямолинейно, вектор ![]() направлен к полюсу А, а вектор
направлен к полюсу А, а вектор ![]() перпендикулярен ему.
Получим два алгебраических уравнения для определения величин и направлений
ускорений
перпендикулярен ему.
Получим два алгебраических уравнения для определения величин и направлений
ускорений ![]() и
и ![]() (вначале направляем
искомые векторы произвольно):
(вначале направляем
искомые векторы произвольно):
![]() ;
;
![]() .
.
Предварительно
вычислим составляющие ускорения согласно формулам :
![]()
![]()
![]()
Далее определим:
– из 2-го уравнения

– из 1-го уравнения
![]()
Знаки
показывают, что направление ускорения ![]() совпадает с принятым,
а направление
совпадает с принятым,
а направление ![]() – противоположно
направлению, указанному на рис. Зная ускорение
– противоположно
направлению, указанному на рис. Зная ускорение ![]() , можно найти угловое ускорение шатуна
, можно найти угловое ускорение шатуна
![]()
15.11. Катушка катится без скольжения в вертикальной плоскости по
наклонному пути (см. рис.).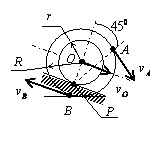 Найти угловую скорость катушки, скорости точек
О и В, если в рассматриваемый
момент времени
Найти угловую скорость катушки, скорости точек
О и В, если в рассматриваемый
момент времени ![]() = 2 м/с, r = 0.6 м, R= 1 м.
= 2 м/с, r = 0.6 м, R= 1 м.
Решение: Катушка совершает плоскопараллельное движение. Так
как качение происходит без скольжения, то скорость точки Р
касания катушки с неподвижной
поверхностью ![]() , следовательно
эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А
, следовательно
эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А ![]() перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости
пропорционально расстоянию от точки А до МЦС:
перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости
пропорционально расстоянию от точки А до МЦС:
![]() ,
,
где![]()
![]() 1,49 м.
1,49 м.
Определим угловую скорость катушки
![]() .
.
Так как скорости точек О и В катушки также пропорциональны их расстояниям до точки Р, то
![]() 0,81 м/с;
0,81 м/с;
![]() = 0,54 м/с.
= 0,54 м/с.
Направление вращения
катушки, а, следовательно, и направления скоростей точек В и О, определяются
направлением вектора скорости ![]() по отношению к МЦС.
по отношению к МЦС.
15.12. Стержень АВ
имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью ![]() = 1 м/с. Найти в
положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С,
если АВ = 1,2 м, АС = ВС.
= 1 м/с. Найти в
положении, указанном на рисунке, угловую скорость стержня, скорости точек В и С,
если АВ = 1,2 м, АС = ВС.
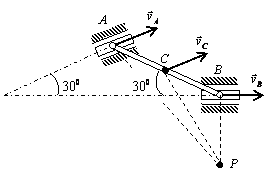
Решение: Стержень АВ совершает плоскопараллельное движение. Так как скорости точек А и В направлены параллельно соответствующим направляющим, вдоль которых скользят ползуны, то, восстанавливая из точек А и В перпендикуляры к скоростям этих точек, определим положение мгновенного центра скоростей стержня АВ – точка Р. Треугольник АВР является равнобедренным, следовательно, АВ = ВР = 1,2м.
Скорость точки
А пропорциональна расстоянию от этой
точки до точки Р: ![]() , где
, где ![]() 2,08 м.
2,08 м.
Вычислим
угловую скорость стержня АВ
![]() .
.
Скорость точки В определим по формуле
![]() = 0,48·1,2 = 0,58 м/с.
= 0,48·1,2 = 0,58 м/с.
Для определения скорости точки С найдем расстояние РС с помощью теоремы косинусов
![]() 1,59 м.
1,59 м.
Тогда скорость точки С
![]() = 0,76 м/с.
= 0,76 м/с.
15.13. Кривошип ОА длиной r = 1 м
вращается с угловой скоростью ![]() = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как
показано на рисунке. Определить скорость ползуна В, угловую скорость шатуна
= 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как
показано на рисунке. Определить скорость ползуна В, угловую скорость шатуна ![]() в двух положениях
механизма, когда угол поворота кривошипа
в двух положениях
механизма, когда угол поворота кривошипа ![]() и
и ![]() .
.
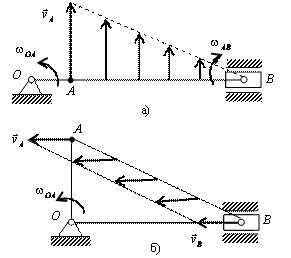
Решение: Шатун АВ совершает плоскопараллельное движение. При этом ![]() , так как точка А
принадлежит кривошипу ОА,
совершающему вращательное движение.
Скорость ползуна В параллельна
направляющим. Численное значение скорости точки А
, так как точка А
принадлежит кривошипу ОА,
совершающему вращательное движение.
Скорость ползуна В параллельна
направляющим. Численное значение скорости точки А
![]() =2·1=2 м/с.
=2·1=2 м/с.
Найдем положение мгновенного центра скоростей,
восстанавливая перпендикуляры к скоростям
точек А и В из этих точек. При угле j = 0 (см. рис. а)
перпендикуляр к скорости ![]() и перпендикуляр к
направлению
и перпендикуляр к
направлению ![]() пересекаются в точке В. Следовательно, точка В является в этом положении механизма
мгновенным центром скоростей и
пересекаются в точке В. Следовательно, точка В является в этом положении механизма
мгновенным центром скоростей и ![]() . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
. Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
![]() = 0,5 рад/с.
= 0,5 рад/с.
На рис. а показано распределение скоростей точек шатуна.
При угле поворота кривошипа j = 900
скорости ![]() и
и ![]() направлены
параллельно, а перпендикуляры к ним пересекаются в бесконечности.
Следовательно, в данный момент времени
имеет место мгновенное поступательное распределение скоростей, то есть все
точки шатуна АВ имеют одинаковые
скорости, равные
направлены
параллельно, а перпендикуляры к ним пересекаются в бесконечности.
Следовательно, в данный момент времени
имеет место мгновенное поступательное распределение скоростей, то есть все
точки шатуна АВ имеют одинаковые
скорости, равные ![]() , при этом угловая скорость шатуна
, при этом угловая скорость шатуна ![]() (рис. б).
(рис. б).
15.14.
Кривошип ОА = 0,5м вращается с угловой скоростью ![]() = 10 рад/с и приводит
в движение шатун АВ = 4 м. Найти угловую
скорость шатуна, скорости точек В и С (АС = 2,5м),
если угол поворота кривошипа
= 10 рад/с и приводит
в движение шатун АВ = 4 м. Найти угловую
скорость шатуна, скорости точек В и С (АС = 2,5м),
если угол поворота кривошипа ![]() и
и ![]() (см. рис.).
(см. рис.).
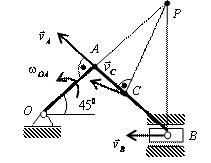
Решение: Так как кривошип ОА совершает вращательное движение, то
![]()
Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.
Найдем угловую скорость шатуна АВ
![]() .
.
Скорости точек В и С пропорциональны их расстояниям до МЦС:
![]() ,
,
где
ВР =![]()
![]() 5,65 м;
5,65 м;
![]() = 1,25·5,65 = 7,07 м/с;
= 1,25·5,65 = 7,07 м/с;
![]() ,
,
где СР
=![]()
![]() 4,72 м;
4,72 м;
![]() =
1,25·4,72 = 5,9 м/с.
=
1,25·4,72 = 5,9 м/с.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Строительная механика Сопротивление материалов
Прикладная механика Детали машин
Теория
машин и механизмов