Главная

Лекция 8. Принцип возможных перемещений и общее уравнение динамики.

В данной лекции рассматриваются следующие вопросы:

1. Возможные перемещения. Классификация связей.

2. Принцип возможных перемещений при равновесии материальной системы. Общее уравнение статики.

3. Принцип возможных перемещений при движении материальной системы. Общее уравнение динамики

4. Обобщенные координаты.

5. Обобщенные силы.

6. Уравнения равновесия Лагранжа.

7. Обобщенные силы инерции.

8. Уравнения Лагранжа.

Изучение данных вопросов необходимо для изучения демпферов в дисциплине «Детали машин», для решения задач в дисциплинах «Теория машин и механизмов» и «Сопротивление материалов».

Аналитическая механика построена на некоторых основных началах (принципах), которые предлагают свои (отличные от ранее рассмотренных) подходы и методы решения задач механики.

Классическая механика в основном оперирует векторными величинами, векторными равенствами, а алгебраические уравнения получаются в результате проецирования векторных равенств на координатные оси. В расчетных уравнениях аналитической механики широко применяются скалярные энергетические характеристики движения материальных объектов и скалярные меры действия на них систем сил.

Характерным для системы изложения аналитической механики является то, что ее основу составляют некоторые общие принципы, из которых аналитическим путем получаются дифференциальные уравнения движения.

Методы аналитической механики оказались плодотворными не только в теоретических исследованиях, но и в практических инженерных расчетах, так как они предоставили универсальный аналитический инструментарий для решения сложных задач.

Возможные перемещения. Классификация связей.

Связями называются любого вида ограничения, налагаемые на положения и скорости точек механической системы, причем они должны выполняться при любых действующих на систему силах. Конструктивно связи осуществляются в виде нитей, стержней, шарниров, поверхностей и т. д. Аналитически наличие связей выражается уравнениями, связывающими у механической системы координаты точек, их скорости и время.

При изучении равновесия системы тел методами так называемой геометрической статики приходится рассматривать равновесие каждого из тел в отдельности, заменяя наложенные связи соответствующими наперед неизвестными реакциями. Когда число тел в системе велико, этот путь становится весьма громоздким и связан с необходимостью решать большое число уравнений со многими неизвестными.

Отличительная особенность метода, вытекающего из принципа возможных перемещений, состоит в том, что при его применении эффект действия связей учитывается не путем введения неизвестных наперед реакций, а путем рассмотрения перемещений, которые можно сообщить точкам системы, если вывести систему из занимаемого ею положения. Эти перемещения называют в механике возможными перемещениями.

Рассмотрим возможные перемещения точки М на стержне, прикрепленном к неподвижной поверхности шарниром О (рис.2,а). Конечно, стержень позволяет точке двигаться по сферической поверхности в любом направлении и на любое расстояние. Все эти перемещения возможны. Возможно, кстати, перемещение и вниз. Но такое перемещение не стоит называть возможным, потому что нарушается связь, стержень.

В аналитической механике эффект действия связей на механическую систему определяется не только реакциями связей, но и влиянием связей на подвижность системы, что характеризуется картиной тех бесконечно малых перемещений, которые могут осуществляться при наличии связей.

Кроме того, возможным перемещением будем называть только малое перемещение, настолько малую часть траектории, что ее можно заменить прямой, отрезком касательной.

Теперь можно сформулировать определение возможного перемещения.

Возможным перемещением точки материальной системы будем называть ее бесконечно малое перемещение, допускаемое связями этой системы.

Возможным перемещением механической системы называют любую совокупность возможных перемещений точек этой системы, допускаемую всеми наложенными на нее связями.

Возможные перемещения точки отражают особенности наложенных на точку связей, их нельзя смешивать с ее действительным перемещением. Так, если точка лежит на плоскости, то ее возможными перемещениями являются бесконечно малые перемещения в любом направлении по этой плоскости. Действительным же перемещением точки может быть лишь одно из этих возможных, именно то, которое обусловлено не только характером связи, но и действующими на точку силами, ее массой, начальными условиями ее движения.

Возможные перемещения точек системы должны удовлетворять двум условиям:

1) они должны быть бесконечно малыми, так как при конечных перемещениях система перейдет в другое положение, где условия равновесия могут быть другими;

2) они должны быть такими, чтобы при этом все наложенные на систему связи сохранялись, так как иначе мы изменим, вид рассматриваемой механической системы (система станет другой).

Например, для кривошипно-шатунного механизма, изображенного на рис.1 перемещение точек кривошипа ОА в положение ОА₁ нельзя рассматривать как возможное, так как в этом положении условия равновесия механизма под действием сил и будут уже другими. Точно так же нельзя считать возможным даже бесконечно малое перемещение точки В шатуна вдоль линии BD; оно было бы возможным, если в точке В вместо ползуна была бы качающаяся муфта, т.е. когда механизм был бы другим.

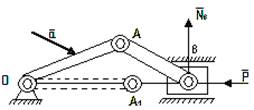
Рис.1

Таким образом, возможным перемещением системы мы будем называть любую совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент всеми наложенными на систему связями. Возможное перемещение любой точки системы будем изображать элементарным вектором , направленным в сторону перемещения.

В общем случае для точек и тел системы может существовать множество возможных различных перемещений (перемещения и мы не считаем разными). Однако для каждой системы, в зависимости от характера наложенных на нее связей, можно указать определенное число таких независимых между собой перемещений, что всякое другое возможное перемещение будет получаться как геометрическая сумма. Например, шарик, лежащий на какой-нибудь плоскости (или поверхности), можно переместить вдоль этой плоскости по множеству направлений. Однако любое его возможное перемещение можно получить как сумму двух перемещений и вдоль лежащих в этой плоскости взаимно перпендикулярных осей ().

Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Так, рассмотренный выше шарик на плоскости (или на поверхности), если его считать материальной точкой, имеет 2 степени свободы. У кривошипно-шатунного механизма будет, очевидно, одна степень свободы.

У свободной материальной точки – 3 степени свободы (независимыми будут 3 перемещения вдоль взаимно перпендикулярных осей). Свободное твердое тело имеет 6 степеней свободы (независимыми перемещениями будут: 3 поступательных перемещения вдоль осей координат и 3 вращательных вокруг этих осей).

К этому следует добавить несколько замечаний.

Первое. Само название таких перемещений показывает, что они только возможны, но не обязательны; что этих перемещений из данного положения системы может быть много; что среди них только одно есть действительное (Если связи – не стационарные, изменяются с течением времени, то действительное перемещение может не быть одним из возможных); что эти перемещения происходят не под действием сил, приложенных к системе, а, так сказать, по нашему желанию.

Второе. За счет малости таких перемещений направляются они по касательной к траектории и имеют, таким образом, направление, совпадающее с вектором скорости. Эту скорость в данном случае также называют возможной скоростью, а не действительной.

Третье. При наличии связей между точками материальной системы, возможные перемещения этих точек связаны между собой определенными зависимостями, уравнениями связей.

На рис.2 дано несколько примеров возможных перемещений точек некоторых материальных систем.

Из этих примеров следует, что возможным перемещением всего тела, вращающегося вокруг оси, является малый угол поворота . И возможные перемещения точек его можно определить с помощью этого угла. Так, например, (рис.2, а и 2, б).

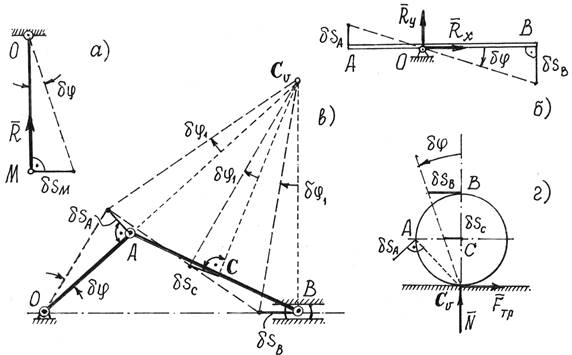
Рис.2

Так как направления возможных перемещений имеют направления скоростей, то перемещения точек звена АВ (рис.2, в) определяются с помощью мгновенного центра скоростей этого звена. А возможное перемещение всего тела при плоскопараллельном движении – есть поворот на малый угол вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.

Так как , то , а перемещение ползуна В: и точки С: . То есть перемещения всех точек механизма можно определить через одно возможное перемещение, перемещение звена ОА, через угол .

Аналогично, поворотом на малый угол вокруг мгновенного центра скоростей , определяются возможные перемещения точек колеса, которое может катиться без скольжения по неподвижной прямой (рис.2, г).

Рассмотрим еще пример. Так, для груза, расположенного на неподвижной плоскости (рис. 2.1, а), таким возможным перемещением будет перемещение вдоль неподвижной плоскости.

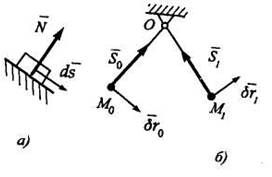
Рис. 2.1

Для точки М стержня ОМ, имеющего цилиндрический шарнир в точке О (рис. 2.1, б), возможным перемещением в положении М_о будет , а в положении M₁ - это будет (эти перемещения, как являющиеся бесконечно малыми, перпендикулярны оси стержня). В точке М_о реакция нити , а в точке М₁ — реакция .

Работу сил, приложенных к материальной системе, на возможном перемещении будем называть возможной работой.

Если рассмотреть различные типы материальных систем, можно обнаружить, что элементарная работа реакций многих связей на возможном перемещении окажется равной нулю. Такие связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями. К таким связям относятся, например, все связи без трения.

Связи, которые не изменяются со временем, называются стационарными. Связи, изменяющиеся со временем называются нестационарными (они реализуются посредством движущихся или деформирующихся тел).

Различают связи геометрические и кинематические (дифференциальные). Первые налагают ограничения только на положения (координаты) точек системы, вторые — налагают ограничения еще и на скорости точек. В соответствии с этим уравнения геометрических связей будут содержать только координаты элементов системы и, может быть, время, т. е. f(x_k, у_к, z_k, t) = 0, а уравнения кинематических связей — содержать первые производные от координат по времени, т. е.

Геометрические и интегрируемые дифференциальные связи называют голономными. Мы в дальнейшем будем рассматривать системы только с голономными связями.

Рассмотрим некоторые примеры.

Связь между точками абсолютно твердого тела, которая не позволяет изменять расстояния между любыми двумя его точками, является геометрической стационарной связью. Ее уравнение будет (x₂ - x₁)² + (y₂ – y₁)² + (z₂ - z_l)² - l² = 0, где х_1, у_1, z_1, x₂, у₂, z₂ — координаты точек 1 и 2, l — расстояние между этими точками. Таковыми же являются связи в виде неподвижных гладкой плоскости, подпятника.

На рис. 2.2 точка М движется внутри вращающейся трубки. По отношению к неподвижной системе координат внутренняя поверхность трубки будет для точки М являться нестационарной геометрической связью (координаты х_м и у_м будут зависеть от времени t).

Рис. 2.2

Аналогичное можно сказать о связи точки М на рис.2.3 и о связи точки D на рис.2.4.

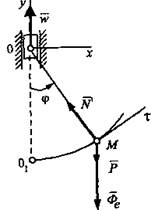
Рис.2.3

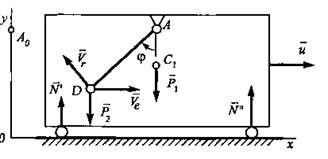
Рис.2.4

Также различают связи удерживающие (двусторонние) и неудерживающие (односторонние). Удерживающие связи налагают на систему (точку) ограничения, которые сохраняются при любом положении системы и любых действующих на нее силах.

Так, для точки С физического маятника (рис.2.5, а), жестко соединенной с неподвижным шарниром О, связь является геометрической удерживающей, ее уравнение x² + y² + z² - l² = 0, где l — расстояние ОС; х, у, z — координаты точки С в системе отсчета Oxyz. А для точки С математического маятника (рис. 2.5, б), в котором соединение точки С с шарниром О осуществляется в виде нити, связь является односторонней (нить не удерживает точку С от приближения к шарниру О и в этом случае точка С освобождается от связи); математически рассмотренная связь выражается неравенством x² + y² + z² – l² ≤ 0.

Рис. 2.5

Принцип возможных перемещений при равновесии материальной системы. Общее уравнение статики.

Пусть материальная система находится в равновесии. Силы, действующие на каждую ее точку, уравновешиваются. Если – равнодействующая всех активных сил, приложенных к i-той точке, а – реакция связей этой точки, то (рис.3)

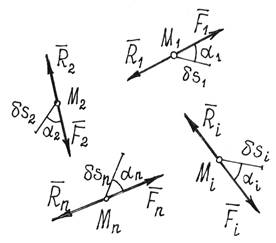
Рис.3

Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения

Затем вычислим работу всех сил на этих перемещениях.

Так как силы, приложенные к каждой точке уравновешиваются и , то сумма работ этих сил на перемещении будет равна нулю: . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю

.

Если связи идеальные, то вторая сумма всегда равна нулю. Значит,

(1)

Этот результат, уравнение работ, называют общим уравнением статики.

Принцип возможных перемещений: При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю.

Конечно, если у системы есть неидеальные связи, например, с трением, или упругие, вроде пружины, то в уравнение работ надо добавить возможную работу реакций этих связей.

Принцип возможных перемещений можно записать в другой форме.

Если возможные перемещения точек определить с помощью возможных скоростей: где время - произвольная бесконечно малая величина, то уравнение работ (1) запишется так , а, поделив его на получим

, (2)

где – углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.

Равенство (2) можно назвать принципом возможных скоростей, уравнением мощностей. Оно иногда бывает более удобным, так как используются конечные величины скоростей, а не бесконечно малые перемещения.

Этот принцип, общее уравнение статики, позволяет решать задачи на исследование равновесного состояния системы, в частности – находить неизвестные реакции связей. Естественно, при этом возникает вопрос: как же так, ведь реакции идеальных связей не входят в уравнение работ? Выход прост – надо сделать тело свободным, реакции отнести к разряду активных сил и затем назначать такие возможные перемещения, чтобы эти неизвестные силы совершали работу.

Общее уравнение статики – довольно эффективный метод и применять его, конечно, надо для исследования равновесия сложных систем; хотя и при решении обычных задач статики он оказывается тоже выгодным.

В качестве важного достоинства отметим, что применение принципа возможных перемещений не требует рассмотрения равновесия отдельных частей (тел) механической системы и позволяет исключить из рассмотрения все наперед неизвестные реакции идеальных связей. Отметим еще, что при решении задач на равновесие механической системы с помощью принципа возможных перемещений число расчетных уравнений равно числу степеней свободы системы.

Это преимущество особенно заметно, когда находящаяся в равновесии система состоит из большого числа связанных между собой тел. Решение задачи о равновесии такой системы методами геометрической статики предусматривает расчленение системы на отдельные тела и составление уравнений равновесия этих тел (в эти уравнения войдут и силы взаимодействия между телами, реакции внешних связей), что приводит к составлению большого числа уравнений со многими неизвестными. Применяя принцип возможных перемещений для системы с многими телами, но имеющей одну степень свободы (что часто бывает в практических задачах), получим условие равновесия в виде одного уравнения работ (1); причем реакции идеальных связей можно из рассмотрения исключить (и на чертеже не изображать). К системам с неидеальными связями в общем случае принцип возможных перемещений неприменим. Однако в некоторых случаях, например при движении тела по шероховатой поверхности эту неидеальную связь можно рассматривать как идеальную, включив силу трения в число активных сил.

Пример 1. Какую силу F надо приложить к желобу с грузом весом Р, чтобы удержать его в равновесии (рис.4)?

Рис.4

Решение. Эту задачу можно решить известными методами статики, составляя уравнения равновесия. Но при этом придется прежде отыскать усилия в стержнях. Принцип возможных перемещений позволяет найти силу F проще, с помощью общего уравнения статики.

Показываем активные силы и . Даем системе возможное перемещение, повернув стержень АО на угол (рис.66). Так как желоб совершит поступательное движение, то перемещения всех его точек будут одинаковы:

где a=AO=BD.

Составляем уравнение работ: . Угол .

Поэтому получим . Отсюда .

Пример 2. На рис.5 изображена конструкция, состоящая из четырех одинаковых Т-образных рам, соединенных шарнирами К, М, Q. Опоры А и Е – шарнирно-неподвижные, В и D – шарнирно-подвижные. Определим горизонтальную составляющую реакции опоры Е, вызванную силой , приложенной к левой раме.

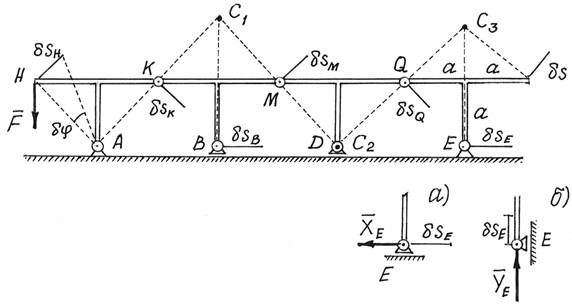
Рис.5

Решение. Методы статики дадут довольно сложное и длинное решение, так как придется рассматривать равновесие четырех рам и решать систему из 12 уравнений с 12-ю неизвестными.

Принцип возможных перемещений дает более простое и короткое решение.

Надо изменить конструкцию опоры Е. Сделаем ее подвижной, а чтобы система осталась в равновесии, приложим к опоре силу , ту силу, которую нужно определить (рис.5,а).

Даем затем системе возможное перемещение, повернув левую раму вокруг опоры А на угол . С помощью мгновенных центров скоростей С1, С2 и С3 каждой рамы, обнаруживаем, что , а или Составляем уравнение работ, общее уравнение статики, или . Отсюда .

Чтобы определить вертикальную составляющую реакции опоры Е, ее надо вновь переделать (рис. 5,б), дать системе соответствующее возможное перемещение и составить уравнение работ.

Пример 3. Для механизма, расположенного в горизонтальной плоскости (рис.5.1,а) , определить деформацию пружины в положении равновесия. Даны длина стержня OA = l, момент пары сил М, приложенной к стержню OA, коэффициент жесткости пружины С.

а)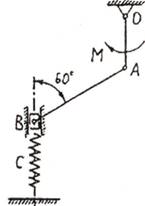 б)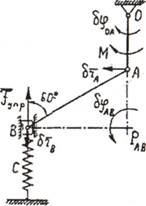

Рис.5.1

Решение. Для решения задачи будем использовать принцип возможных перемещений.

Приложим к системе силы, действующие в горизонтальной плоскости: кроме пары с моментом М это будет сила упругости пружины F_упр = сх (х - искомая деформация пружины) (рис.5.1,б).

Сообщим системе возможное перемещение, повернув стержень OA на угол δφ_ОА. Стержень АВ совершит возможное плоскопараллельное перемещение, повернувшись на угол δφ_АВ вокруг точки Р_АВ. Точки А и В получат возможные перемещения

Составим уравнение возможных работ всех активных сил

Подставив установленные ранее соотношения, получим

Откуда деформация пружины

Пример 4. Для заданной составной конструкции (рис.5.2,а) определить реактивный момент в заделке А, считая заданными интенсивность равномерно распределенной нагрузки q, угол α, длины стержней AB=l; BC = l₂.

а)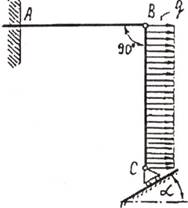 б)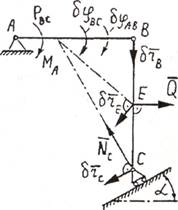

Рис.5.2

Решение. Для решения задачи используем принцип возможных перемещений.

Заменим заделку в точке А шарнирно неподвижной опорой, компенсировав отброшенную связь ее реакцией — реактивной парой сил с неизвестным моментом М_А (рис.5.2,б).

Распределенную нагрузку на участке ВС заменим приложенной к точке Е равнодействующей силой Q = ql₂,; BE = ЕС =l₂/2.

Сообщим системе возможное перемещение, повернув стержень АВ на угол δφ_АВ. Стержень ВС совершит возможное плоскопараллельное перемещение, повернувшись на угол δφ_ВС вокруг точки Р_вс. Точки В, С и Е получат соответствующие возможные перемещения

Уравнение возможных работ имеет вид

Далее находим

Окончательно получим

Принцип возможных перемещений при движении материальной системы. Общее уравнение динамики.

По принципу Даламбера материальную систему, движущуюся под действием некоторых сил, можно рассматривать находящейся в равновесии, если ко всем точкам системы приложить их силы инерции. Значит можно воспользоваться и принципом возможных перемещений.

В уравнение работ (1) добавится еще сумма работ сил инерции точек на их возможных перемещениях:

. (3)

Или по принципу возможных скоростей (2):

(4)

Эти уравнения называют общим уравнением динамики. Оно позволяет решать большой класс задач на исследование движения довольно сложных материальных систем.

Уравнения (3) и (4) показывают, что в любой фиксированный момент времени сумма элементарных работ активных сил и сил инерции на любых виртуальных перемещениях равна нулю при условии, что на систему наложены идеальные и удерживающие связи (принцип Даламбера-Лагранжа).

Силы инерции точек и твердых тел, составляющих систему, определять уже умеем.

Стоит подчеркнуть еще одно важное достоинство этого метода, общего уравнения динамики, – реакции связей (идеальных) исключаются при исследовании движения системы.

Иногда это уравнение можно использовать для исследования движения механических систем и в тех случаях, когда не все связи являются идеальными, например, когда имеются связи с трением. Для этого следует к активным силам добавить те составляющие реакций, которые обусловлены наличием сил трения.

Рассмотрим процедуру использования уравнения (3) для составления дифференциальных уравнений движения систем с двумя степенями свободы:

1. Изобразить механическую систему в произвольный момент времени.

2. Показать на рисунке активные силы и моменты, а также силы и моменты, соответствующие неидеальным связям (например, силы трения).

3. Определить главные векторы и главные моменты сил инерции.

4. Выбрать обобщенные координаты в числе, равном числу степеней свободы системы.

5. Дать виртуальное перемещение, соответствующее одной из степеней свободы системы, считая при этом виртуальные перемещения, соответствующие остальным степеням свободы, равными нулю.

6. Вычислить сумму элементарных работ всех сил и моментов (см. п. 2 и 3) на соответствующих виртуальных перемещениях и приравнять эту сумму нулю.

7. Повторить п. 4 - 6 для каждого независимого движения системы.

При применении общего уравнения динамики к системам с двумя и большим числом степеней свободы, в связи с громоздкостью выкладок, можно использовать следующие рекомендации:

1. Сделать предположение о направлении ускорений точек системы.

2. Направить на рисунке силы инерции в стороны, противоположные выбранным направлениям соответствующих ускорений.

3. Определить знаки элементарных работ сил инерции в соответствии с их направлениями на рисунке и избранными направлениями виртуальных перемещений точек системы.

4. Если искомые ускорения оказываются положительными, то сделанные предположения о направлениях ускорений подтверждаются, если отрицательными, то соответствующие ускорения направлены в другую сторону.

Пример 5. Определим ускорение груза G (рис.6). Вес цилиндра – Р, радиус – r. Цилиндр катится по плоскости без скольжения.

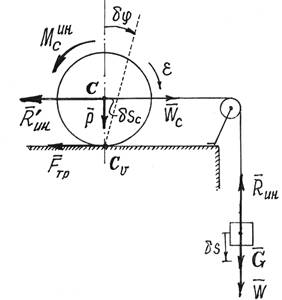
Рис.6

Решение. Показываем задаваемые силы – . Добавляем силы инерции. Сила инерции груза, движущегося поступательно,

.

Цилиндр совершает плоскопараллельное движение. Главный вектор сил инерции точек его

Главный момент сил инерции относительно центральной оси С:

Даем системе возможное перемещение, сдвинув груз вниз на малую величину . Центр цилиндра сместится вправо на величину , а весь цилиндр повернется вокруг мгновенного центра скоростей на угол

Вычисляем работу сил на этих перемещениях и составляем уравнение работ, общее уравнение динамики,

Так как , то, подставив значения сил инерции, получим уравнение

из которого находим

Пример 6. Три одинаковых ролика массой m₁, и радиусом r каждый перемещают горизонтальную плиту массой т (рис.6.1,а). Ко всем роликам приложены равные вращающие моменты М. Определить ускорение плиты при условии, что она движется по роликам без проскальзывания. Ролики считать сплошными однородными цилиндрами.

а)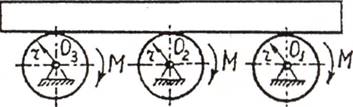 б)

Рис.6.1

Решение. Для решения будем использовать общее уравнение динамики.

Принимаем, что ускорение плиты равно а, а ее возможное перемещение δs. Тогда угловое ускорение каждого ролика ε=a/R, а его возможное угловое перемещение δε= δs/R.

К плите и роликам приложим вес mg и m₁g, вращающие моменты М, силу инерции плиты Ф = та и моменты сил инерции роликов

Для данной системы имеем общее уравнение динамики имеет вид

Далее получаем

Откуда

Пример 7. Постоянный вращающий момент М_вр приложен к барабану лебедки радиуса r и массы m (рис.6.2,а). К концу А троса прикреплен груз массы m₁ который поднимается по наклонной плоскости с углом α. Определить ускорение груза, пренебрегая трением между грузом и наклонной плоскостью. Барабан лебедки считать однородным круглым цилиндром.

а)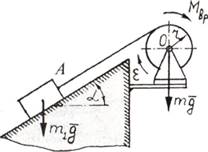 б)

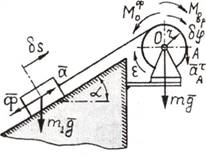
Рис.6.2

Решение. На рис. 6.2,б mg, m₁g — силы тяжести барабана лебедки и груза; М_вр — вращающий момент; Ф — сила инерции груза; - момент сил инерции точек барабана; δs — возможное перемещение груза; δφ - возможное угловое перемещение барабана.

На основании общего уравнения динамики имеем

Воспользуемся зависимостями

где a - ускорение груза; ε - угловое ускорение барабана; J₀ — момент инерции барабана относительно оси вращения.

С учетом указанных выше зависимостей находим ускорение груза

Пример 8. К зубчатой рейке массы m приложена сила Т (рис.6.3,а). Рейка приводит в движение зубчатое колесо радиуса r и массы т₁, к которому приложен момент сопротивления М_c. Определить угловое ускорение колеса, считая его однородным диском.

а)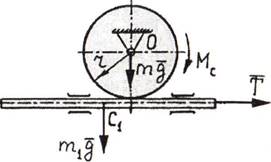 б)

Рис.6.3

Решение. Рейка совершает поступательное движение с ускорением а, зубчатое колесо - вращательное движение с угловым ускорением ε (рис.6.3,б).

Приложим к звеньям механизма силы mg, m₁g, и моменты М_c и .

При сообщении рейке возможного поступательного перемещения δs колесо получит возможное вращательное перемещение δφ.

Общее уравнение динамики имеет вид

Имеют место следующие зависимости

где а - ускорение рейки; ε - угловое ускорение колеса; J_o - момент инерции колеса относительно оси вращения

Используя указанные выше зависимости, определяем угловое ускорение колеса

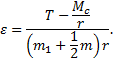
Обобщенные координаты

Свободная в пространстве точка имеет три степени свободы (она обладает тремя независимыми перемещениями), и ее положение в пространстве можно определить тремя независимыми параметрами, например декартовыми координатами х, у, z.

Независимые между собой параметры (координаты), число которых равно числу степеней свободы системы и которые однозначно определяют ее положение, называют обобщенными координатами системы.

В качестве обобщенных координат (их в общем виде обозначают буквой q) можно выбирать параметры, имеющие любой геометрический (или физический) смысл, и соответственно этому они будут иметь разные размерности. Например, стержень ОА, вращающийся в вертикальной плоскости (рис. 7, а), имеет одну степень свободы, и его положение может быть определено на выбор одной из следующих обобщенных координат: 1) q = 𝜑 - А₀А угол поворота стержня ОА от вертикали; 2) q=s_A - длина дуги А₀А; 3) q = 𝜎 - площадь сектора ОА₀А и т. д. Система, изображенная на рис. 7,б, состоит из вращающейся в вертикальной плоскости трубки ОА и ползуна D, прикрепленного к точке О пружиной и двигающегося вдоль трубки. Эта система имеет две степени свободы, ее положение определяется двумя обобщенными координатами, например, такими: q₁ =φ - угол поворота трубки ОA, q₂= s — расстояние OD.

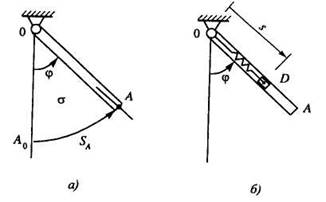
Рис. 7

Так на рис.7.1 положение балочки АВ и всех ее точек вполне определяется углом .

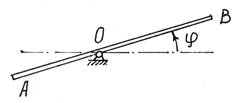
Рис.7.1

Положение точек кривошипно-шатунного механизма (рис.8) можно определить заданием угла поворота кривошипа или расстоянием s, определяющим положение ползуна В (при ).

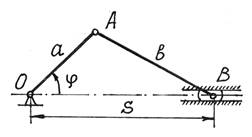
Рис.8

Положение сферического маятника (рис.9) определяется заданием двух параметров, углов и .

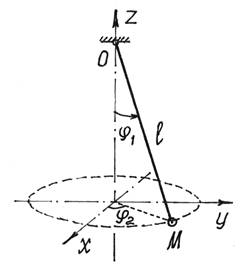
Рис.9

У свободного твердого тела шесть степеней свободы (независимые перемещения: три поступательных вдоль координатных осей и три поворота вокруг этих осей), и его положение в пространстве определяется шестью параметрами: например, тремя координатами точки, принятой за полюс, и тремя угловыми координатами (углами Эйлера).

Обобщая изложенное выше, заметим, что у механической системы с геометрическими связями число независимых возможных перемещений, число обобщенных координат и число степеней свободы является одним и тем же числом, характеризующим подвижность этой системы в пространстве.

Введение понятия обобщенных координат позволяет положение даже сложных механических систем (с большим количеством тел и связей) определять лишь некоторым числом параметров. Поэтому количество дифференциальных уравнений движения системы в обобщенных координатах, как правило, меньше, чем в декартовых координатах. Многие механизмы и машины, состоящие из многих тел, представляют собой системы с одной степенью свободы, и для определения их положений достаточно задать одну обобщенную координату.

Минимальное количество независимых друг от друга обобщенных координат, которых достаточно, чтобы полностью и однозначно определить положение всех точек системы, называют числом степеней свободы этой системы.

Вообще для любой материальной системы можно назначить несколько обобщенных координат. Например, у кривошипно-шатунного механизма (рис.8) указаны две обобщенные координаты и s. Но это не значит, что у механизма две степени свободы, так как одну координату можно определить через другую:

.

А вот у маятника (рис.9) две степени свободы, т.к. определяется его положение двумя независимыми обобщенными координатами. Кстати, если длина маятника изменяется, то для определения положения точки М потребуется еще один параметр – обобщенная координата l , длина нити. И у маятника станут три степени свободы.

Пусть материальная система имеет s степеней свободы. Положение ее определяется обобщенными координатами: q₁, q₂, q₃,…, q_k,…, q_{s. .}

Нетрудно убедиться, что декартовы координаты n точек системы можно определить как функции обобщенных координат и времени:

Так у маятника (рис.9) координаты точки М

есть функции координат l, и , и времени t, если l = l(t).

Соответственно, и радиус-вектор точек системы можно определить как функцию обобщенных координат и времени:

(6)

Обобщенные силы

Каждой обобщенной координате можно вычислить соответствующую ей обобщенную силу Q_k.

Вычисление производится по такому правилу.

Чтобы определить обобщенную силу Q_k, соответствующую обобщенной координате q_k, надо дать этой координате приращение (увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты :

где – перемещение i-той точки системы, полученное за счет изменения k–той обобщенной координаты.

Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:

И так как есть приращение радиуса-вектора за счет приращения координаты при остальных неизменных координатах и времени t, отношение можно определять как частную производную . Тогда

где координаты точек – функции обобщенных координат (5).

Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых , где а координаты точек – функции обобщенных координат, то

Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.

Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат

П = П(q₁, q₂, q₃,…,q_s).

Замечания.

Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.

Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты. Так если размерность [q] – метр, то размерность

[Q]= Нм/м = Ньютон, если [q] – радиан, то [Q] = Нм; если [q] = м², то [Q]=H/м и т.п.

Пример 9. По качающемуся в вертикальной плоскости стержню скользит колечко М весом Р (рис.10). Стержень считаем невесомым. Определим обобщенные силы.

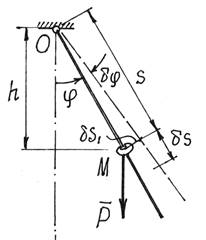
Рис.10

Решение. Система имеет две степени свободы. Назначаем две обобщенные координаты s и .

Найдем обобщенную силу, соответствующую координате s. Даем приращение этой координате, оставляя координату неизменной, и вычислив работу единственной активной силы Р, получим обобщенную силу

Затем даем приращение координате , полагая s = const. При повороте стержня на угол точка приложения силы Р, колечко М, переместится на . Обобщенная сила получится

Так как система консервативная, обобщенные силы можно найти и с помощью потенциальной энергии . Получим и . Получается гораздо проще.

Уравнения равновесия Лагранжа

По определению (7) обобщенные силы , k = 1,2,3,…,s, где s – число степеней свободы.

Если система находится в равновесии, то по принципу возможных перемещений (1) . Здесь – перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все ее обобщенные силы равны нулю:

Q_k = 0, (k=1,2,3,…, s). (10)

Эти уравнения, уравнения равновесия в обобщенных координатах или уравнения равновесия Лагранжа, позволяют решать задачи статики еще одним методом.

Уравнения Лагранжа дают единый и притом достаточно простой метод решения задач динамики как для простых, так и для сложных механических систем. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел (или точек), входящих в систему, ни от того, как эти тела движутся.

Если система консервативная, то . Значит, в положении равновесия . То есть в положении равновесия такой материальной системы ее потенциальная энергия либо максимальна, либо минимальна, т.е. функция П(q) имеет экстремум.

Это очевидно из анализа простейшего примера (рис.11). Потенциальная энергия шарика в положении М₁ имеет минимум, в положении М₂ – максимум. Можно заметить, что в положении М₁ равновесие будет устойчивым; в положении М₂ – неустойчивым.

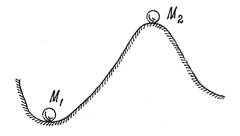
Рис.11

Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние и эти отклонения в дальнейшем не увеличатся.

Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.

Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется, второй производной, ее значением в положении равновесия,

. (11)

Пример 10. Стержень ОА весом Р может вращаться в вертикальной плоскости вокруг оси О (рис.12). Найдем и исследуем устойчивость положений равновесия.

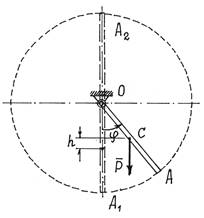
Рис.12

Решение. Стержень имеет одну степень свободы. Обобщенная координата – угол .

Относительно нижнего, нулевого, положения потенциальная энергия П=Рh или

В положении равновесия должно быть . Отсюда имеем два положения равновесия, соответствующие углам и (положения ОА₁ и ОА₂). Исследуем их устойчивость. Находим вторую производную . Конечно, при , . Положение равновесия устойчиво. При , . Второе положение равновесия – неустойчиво. Результаты очевидны.

Обобщенные силы инерции

По той же методике (8), по которой вычислялись обобщенные силы Q_k, соответствующие активным, задаваемым, силам, определяются и обобщенные силы S_k, соответствующие силам инерции точек системы:

И, так как то

Немного математических преобразований.

Очевидно,

Отсюда

Так как а qk = qk(t), (k = 1,2,3,…, s), то

Значит, частная производная скорости по

Кроме того, в последнем члене (14) можно поменять порядок дифференцирования:

Подставляя (15) и (16) в (14), а потом (14) в (13), получим

Разделив последнюю сумму на две и, имея ввиду, что сумма производных равна производной от суммы, получим

где – кинетическая энергия системы, - обобщенная скорость.

Уравнения Лагранжа

По определению (7) и (12) обобщенные силы

Но на основании общего уравнения динамика (3), правая часть равенства равна нулю. И так как все (k = 1,2,3,…,s) отличны от нуля, то . Подставив значение обобщенной силы инерции (17), получим уравнение

Эти уравнения называются дифференциальными уравнениями движения в обобщенных координатах, уравнениями Лагранжа второго рода или просто – уравнениями Лагранжа.

Количество этих уравнений равно числу степеней свободы материальной системы.

Если система консервативная и движется под действием сил потенциального поля, когда обобщенные силы , уравнения Лагранжа можно составить по форме

Или

где L = T – П называется функцией Лагранжа (предполагается, что потенциальная энергия П не зависит от обобщенных скоростей).

Нередко при исследовании движения материальных систем оказывается, что некоторые обобщенные координаты q_j не входят явно в функцию Лагранжа (или в Т и П). Такие координаты называют циклическими. Уравнения Лагранжа, соответствующие этим координатам, получаются проще.

.

Первый интеграл таких уравнений находится сразу. Он называется циклическим интегралом:

Дальнейшие исследования и преобразования уравнений Лагранжа составляют предмет специального раздела теоретической механики – «Аналитическая механика».

Уравнения Лагранжа обладают целым рядом достоинств в сравнении с другими способами исследования движения систем. Основные достоинства: методика составления уравнений одинакова во всех задачах, реакции идеальных связей не учитываются при решении задач.

И еще одно – эти уравнения можно использовать для исследования не только механических, но и других физических систем (электрических, электромагнитных, оптических и др.).

Пример 11. Продолжим исследование движение колечка М на качающемся стержне (пример 9).

Обобщенные координаты назначены – и s (рис.13). Обобщенные силы определены: и .

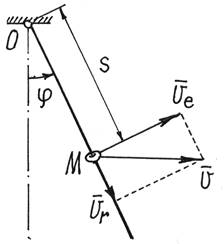
Рис.13

Решение. Кинетическая энергия колечка Где а и .

Поэтому

Составляем два уравнения Лагранжа

то уравнения получаются такими:

или

Получили два нелинейных дифференциальных уравнения второго порядка, для решения которых нужны специальные методы.

Пример 12. Составим дифференциальное уравнение движения балочки АВ, которая перекатывается без скольжения по цилиндрической поверхности (рис.14). Длина балочки АВ = l, вес – Р.

В положении равновесия балочка располагалась горизонтально и центр тяжести С ее находился на верхней точке цилиндра. Балочка имеет одну степень свободы. Положение ее определяется обобщенной координатой – углом (рис.14).

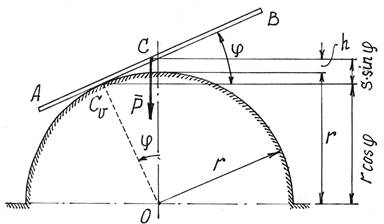
Рис.14

Решение. Система консервативная. Поэтому уравнение Лагранжа составим с помощью потенциальной энергии П=mgh, вычисленной относительно горизонтального положения. В точке касания находится мгновенный центр скоростей и ( равно длине дуги окружности с углом ).

Поэтому (см. рис.76) и .

Кинетическая энергия (балка совершает плоскопараллельное движение)

Находим необходимые производные для уравнения и

Составляем уравнение

или, окончательно,

Вопросы для самопроверки

- Что называется возможным перемещением несвободной механической системы?

- Как взаимосвязаны возможные и действительные перемещения системы?

- Какие связи называются: а) стационарными; б) идеальными?

- Сформулируйте принцип возможных перемещений. Запишите его формульное выражение.

- Приведите примеры применения принципа возможных перемещений к определению связей и к простейщим машинам ((рычаг, наклонная плоскость и т.д.).

- Возможно ли применение принципа виртуальных перемещений к системам с неидеальными связями?

- Сформулируйте общее уравнение динамики.

- Соединением каких принципов является общее уравнение динамики?

- Что представляют собой обобщенные координаты механической системы?

- Чему равно число степеней свободы механической системы?

- Какая связь между числом степеней свободы механической системы и числом ее обобщенных координат?

- В каком случае декартовы координаты точек системы зависят не только от обобщенных координат, но и от времени?

- Что называют возможными перемещениями механической системы?

- Зависят ли возможные перемещения от действующих на систему сил?

- Какие связи механической системы называют идеальными?

- Почему связь, осуществленная с трением, не является идеальной связью?

- Как формулируется принцип возможных перемещений?

- Какие виды может иметь уравнение работ?

- Почему принцип возможных перемещений упрощает вывод условий равновесия сил, приложенных к несвободным системам, состоящим из большого числа тел?

- Как составляются уравнения работ для сил, действующих на механическую систему с несколькими степенями свободы?

- Какова зависимость между движущей силой и силой сопротивления в простейших машинах?

- Как формулируется золотое правило механики?

- Каким образом определяют реакции связей с помощью принципа возможных перемещений?

- Какие связи называются голономными?

- Что называется числом степеней свободы механической системы?

- Что называется обобщенными координатами системы?

- Сколько обобщенных координат имеет несвободная механическая система?

- Сколько степеней свободы имеет управляемое колесо автомобиля?

- Что называется обобщенной силой?

- Запишите формулу, выражающую полную элементарную работу всех приложенных к системе сил в обобщенных координатах.

- Как определяется размерность обобщенной силы?

- Как вычисляются обобщенные силы в консервативных системах?

- Какие способы вычисления обобщенных сил вы знаете?

- Как вычисляются обобщенные силы в случае сил, имеющих потенциал?

- Запишите одну из формул, выражающих общее уравнение динамики системы с идеальными связями. Каков физический смысл этого уравнения?

- Что называется обобщенной силой активных сил, приложенных к системе?

- Что такое обобщенная сила инерции?

- Сформулируйте принцип Даламбера в обобщенных силах.

- Какой вид имеет общее уравнение динамики?

- Что называется обобщенной силой, соответствующей некоторой обобщенной координате системы, и какую она имеет размерность?

- Чему равны обобщенные реакции идеальных связей?

- Выведите общее уравнение динамики в обобщенных силах.

- Какой вид имеют условия равновесия сил, приложенных к механической системе, полученные из общего уравнения динамики в обобщенных силах?

- Какими формулами выражаются обобщенные силы через проекции сил на неподвижные оси декартовых координат?

- Как определяются обобщенные силы в случае консервативных и в случае неконсервативных сил?

- Какие связи называются геометрическими?

- Приведите векторную запись принципа возможных перемещений.

- Назовите необходимое и достаточной условие равновесия механической системы с идеальными стационарными геометрическими связями.

- Каким свойством обладает силовая функция консервативной системы в состоянии равновесия?

- На основании какого уравнения выводятся уравнения Лагранжа второго рода?

- Какой вид имеет уравнение Лагранжа второго рода? Чему равно число этих уравнений для каждой механической системы?

- Запишите систему дифференциальных уравнений Лагранжа второго рода.

- Сколько уравнений Лагранжа второго рода можно составить для несвободной механической системы?

- Зависит ли число уравнений Лагранжа механической системы от количества тел, входящих в состав системы?

- Что называется кинетическим потенциалом системы?

- Для каких механических систем существует функция Лагранжа?

- Функцией каких аргументов является вектор скорости точки, принадлежащей механической системе с s степенями свободы?

- Чему равна частная производная от вектора скорости точки системы по какой-либо обобщенной скорости?

- Функцией каких аргументов является кинетическая энергия системы, подчиненной голономным нестационарным связям?

- Какой вид имеют уравнения Лагранжа второго рода? Чему равно число этих уравнений для каждой механической системы?

- Какой вид принимают уравнения Лагранжа второго рода в случае, когда на систему действуют одновременно консервативные и неконсервативные силы?

- Что представляет собой функция Лагранжа, или кинетический потенциал?

- Какой вид имеют уравнения Лагранжа второго рода для консервативной системы?

- В зависимости от каких переменных величин должна быть выражена кинетическая энергия механической системы при составлении уравнений Лагранжа?

- Как определяется потенциальная энергия механической системы, находящейся под действием сил упругости?

- Сколько координат нужно для описания трех точек в пространстве:

1) 3;

2) 6;

3) 9;

4) n(n-3);

5) 12.

- Сколько координат нужно для описания положения абсолютно твердого тела в пространстве:

1) 3;

2) 6;

3) 9;

4) 12;

5) n(n-1).

- Понятие «числа степеней свободы»:

1) количество координат в декартовой системе;

2) произведение массы тела на его скорость;

3) количество независимых координат, необходимых для определения положения тел или системы тел;

4) количество уравнений, описывающих законы сохранения для данного процесса;

5) оси гироскопа.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00