Главная

Лекция 4. Динамика системы и твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Механическая система. Силы внешние и внутренние.

2. Масса системы.

3. Центр масс.

4. Динамика вращательного движения.

5. Момент инерции системы относительно оси.

6. Радиус инерции.

7. Момент инерции тела относительно параллельных осей.

8. Момент инерции тела относительно произвольной оси.

9. Теорема Гюйгенса-Штейнера.

10. Дифференциальные уравнения движения системы.

11. Теорема о движении центра масс.

12. Теорема об изменении кинетического момента.

13. Закон сохранения движения центра масс.

Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».

Механическая система. Силы внешние и внутренние.

Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.

Материальное абсолютно твердое тело мы также будем рассматривать как систему материальных точек, образующих это тело и связанных между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Классическим примером механической системы является солнечная система, в которой все тела связаны силами взаимного притяжения. Другим примером механической системы может служить любая машина или механизм, в которых все тела связаны шарнирами, стержнями, тросами, ремнями и т.п. (т.е. различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи.

Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих в воздухе самолетов), механическую систему не образует.

В соответствии со сказанным, силы, действующие на точки или тела системы, можно разделить на внешние и внутренние.

Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом - , а внутренние - .

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать движение всей солнечной системы в целом, то сила притяжения Земли к Солнцу будет внутренней; при изучении же движения Земли по её орбите вокруг Солнца та же сила будет рассматриваться как внешняя.

Внутренние силы обладают следующими свойствами:

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы (рис.1) действуют друг на друга с равными по модулю и противоположно направленными силами и , сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

Рис.1

2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю. Действительно, если взять произвольный центр О, то из рис.1 видно, что . Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет:

Из доказанных свойств не следует однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызывать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твердое тело.

Масса системы. Центр масс.

Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему

Средней плотностью тела называют отношение

Плотностью тела в данной точке называют предел

Отсюда,

Если плотность во всех точках тела одинакова, то такое тело называют однородным.

В однородном поле тяжести, для которого g=const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:

В полученные равенства входят только массы материальных точек (частиц), образующих тело, и координаты этих точек. Следовательно, положение точки С (x_C, y_C, z_C) действительно характеризует распределение масс в теле или в любой механической системе, если под понимать соответственно массы и координаты точек этой системы.

Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.

Положение центра масс определяется его радиус-вектором

где - радиус-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.

Пример 1. На горизонтальной поверхности находится клин массы m₂ с углом α к горизонту и на нем брусок массы m₁. Найти ускорение клина. Все поверхности соприкасающихся тел считать гладкими.

Рис.1.1

Решение. В этой задаче брусок скользит по клину вниз, а клин смещается вправо по горизонтальной поверхности.

Рассмотрим движение обоих тел относительно Земли, т.е. в инерциальной системе отсчета.

На брусок действует Земля с силой тяжести m₁g и клин с силой нормального давления N₁₂ (двойные индексы указывают, что на первое тело действует второе).

По второму закону Ньютона в векторной форме имеем:

На клин действуют силы со стороны Земли m₂g, горизонтальной поверхности N₂ и сила нормального давления бруска N₂₁, причем, по третьему закону Ньютона N₂₁ = -N₁₂. Обозначим модули последних сил N.

По второму закону Ньютона для клина запишем:

Поскольку оба тела движутся с разными ускорениями, нужно записать уравнения, связывающие эти ускорения. С этой целью изобразим клин и брусок в двух состояниях.

Рис.1.2

Из рис.1.2 видно, что перемещение бруска относительно Земли ∆r₁ складывается из двух перемещений: бруска относительно клина и вместе с клином ∆r₂: Отсюда, учитывая определение ускорения несложно получить требуемое соотношение: . С учетом уравнения кинематической связи векторное уравнение для бруска примет вид

Запишем это уравнение в проекциях на оси координат. Поскольку нам известно направление ускорения , направим ось х₁ вдоль наклонной плоскости вниз, а перпендикулярно ей - ось y₁.

Проектируя векторное уравнение динамики для клина, оси координат целесообразно выбрать иначе, совместив ось х₂ с вектором ускорения a₂:

Нетрудно увидеть, что в уравнениях (2) и (3) содержатся только две неизвестные величины: a₂ и N. Исключая из этих уравнений N, получим искомое выражение для ускорения клина:

На примере этой задачи рассмотрим, каким образом можно анализировать полученный результат. Во-первых, обычно производится анализ размерности, во-вторых, рассматриваются предельные случаи.

Проверка размерности результата решения данной задачи тривиальна.

Значительно интереснее оценить правдоподобность результата, исследуя предельные случаи.

Пусть m₂>>m₁ (очень тяжелый клин). Тогда т.е. клин неподвижен, что и следовало ожидать из соображений здравого смысла.

Если m₂<<m₁ (тяжелый брусок на очень легком клине),

Пример 2. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок A, чтобы тела 1 и 2 не двигались относительно него? Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен μ. Массы блока и нитей пренебрежимо малы, трения в блоке нет.

Рис.1.3

Решение. Прежде всего попытаемся ответить на вопрос, как будут вести себя бруски при возрастании ускорения а. При a=0 брусок 2 опускается вниз, брусок 1 перемещается вправо. При возрастании ускорения увеличивается взаимодействие бруска 2 с телом А (он сильнее прижимается к телу А) и соответственно растет сила трения. При некотором значении ускорения a=a_min бруски перестают перемещаться относительно тела А. При дальнейшем росте ускорения а может наступить такая ситуация, при которой брусок 1 “поедет” влево, а брусок 2 - вверх. Этому моменту соответствует a_max. В данной задаче требуется найти минимальное ускорение a_min.

В системе отсчета, связанной с Землей (ИСО), на брусок 1 действуют Земля с силой тяжести m₁g, нить с силой T и тело А с силами нормального давления N₁ и трения F_тр1, причем,

(максимальная сила трения покоя).

Рис.1.4

По второму закону Ньютона для бруска 1 запишем

На брусок 2 также действуют Земля с силой тяжести m₂g, нить с силой T и тело А с силами нормального давления N₂ и силой трения F_тр2, причем,

По второму закону Ньютона для бруска 2

Спроектируем векторные уравнения на оси координат и учтем, что m₁=m₂=m:

для бруска 1

для бруска 2

Разрешим систему уравнений относительно a. Из формулы (4) N₁=mg, следовательно, согласно (1), F_тр1=μmg. Подставляя это выражение в уравнение (3), получаем

Учитывая, что согласно (2) и (5) и подставляя это выражение в уравнение (6), преобразуем его к виду

Исключая из (7) и (8) силу Т, находим искомое ускорение:

Динамика вращательного движения.

Рассмотрим вращение абсолютно твердого тела вокруг неподвижной оси ОО (рис.2). Твердое тело можно рассматривать как систему материальных точек, каждая из которых движется по окружности с одинаковой для всех точек угловой скоростью.

Рис.2

Линейная скорость движения каждой точки определяется выражением

V = ωr,

где r – расстояние от точки до оси вращения.

Момент инерции тела относительно оси. Радиус инерции.

Положение центра масс характеризует распределение масс системы не полностью. Например (рис.3), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).

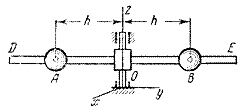
Рис.3

Поэтому в механике вводится еще одна характеристика распределения масс - момент инерции. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

Момент инерции имеет размерность [кг∙м²]

Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.

Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.

Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси, .

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством

где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл. В результате, учитывая, что , где - плотность, а V - объем тела, получим

или

Интеграл здесь распространяется на весь объем V тела, а плотность и расстояние h зависят от координат точек тела.

Моменты инерции некоторых однородных тел:

1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси Аz, перпендикулярной к стержню и проходящей через его конец А (рис.4).

Рис.4

Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса , где - масса единицы длины стержня. В результате

Заменяя здесь ρ₁ его значением, найдем окончательно:

А момент инерции тонкого однородного стержня длины l и массы М относительно оси проходящего через середину и перпендикулярную стержню равен

2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.4,а). Так как все точки кольца находятся от оси Cz на расстоянии h_k=R, то

Следовательно, для кольца .

Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.

3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси Сz, перпендикулярной к пластине и проходящей через ее центр (см. рис.5,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.5,б).

Рис.5

Площадь этого кольца равна , а масса где - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет

,

а для всей пластины . Заменяя здесь его значением, найдем окончательно

Такая же формула получится, очевидно, и для момента инерции однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5,в).

4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:

а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):

г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра): .

Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса-Штейнера.

Моменты инерции данного тела относительно разных осей будут, вообще говоря, разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведенной в теле, найти момент инерции относительно любой другой оси, ей параллельной.

Рис.6

Проведем через центр масс С тела произвольные оси Cx'y'z', а через любую точку О на оси Сх' - оси Oxyz, такие, что Оy||Сy', Oz||Cz' (рис.6). Расстояние между осями Cz' и Оz обозначим через d. Тогда

но, как видно из рисунка, для любой точки тела или , а . Подставляя эти значения , в выражение для и вынося общие множители d ² и 2d за скобки, получим

В правой части равенства первая сумма равна I_cz', а вторая - массе тела М. Найдем значение третьей суммы. На основании формул для координат центра масс .Так как в нашем случае точка С является началом координат, то x_C = 0 и, следовательно, . Окончательно получаем:

Формула выражает следующую теорему Гюйгенса-Штейнера:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

Пример 3. Найти момент инерции системы, состоящей из тонкого стержня массой m₁, длиной l и однородного шара массой m₂, радиусом R относительно оси ОО₁, изображенной на рис.6.1.

Рис.6.1

Решение. Момент инерции обладает свойством аддитивности, то есть момент инерции системы тел равен сумме моментов инерции отдельных тел, входящих в систему: J=J₁+J₂.

В данном случае система тел включает стержень и шар. Момент инерции стержня относительно оси, проходящей через его конец, и момент инерции шара относительно оси, проходящей через его центр, Однако шар вращается вокруг оси, расположенной на расстоянии d=R+l от его центра. Поэтому для расчета момента инерции шара необходимо применять теорему Штейнера: Момент инерции системы

Пример 4. Обруч радиусом R =1 м висит на гвозде, вбитом в стену, и совершает колебания в вертикальной плоскости. Найти период колебаний обруча.

Решение. Обруч представляет собой физический маятник, период колебаний которого можно найти по формуле

где m - масса обруча, I - момент инерции обруча относительно точки подвеса, x - расстояние между точкой подвеса и центром масс.

Момент инерции I найдем по теореме Штейнера

Расстояние x=R. Тогда период колебаний

Момент инерции тела относительно произвольной оси.

Найдем момент инерции тела относительно оси u, проходящей через некоторую точку О (рис. 7).

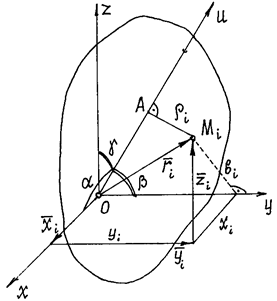
Рис.7

По определению момент инерции .

Поместим в точку О начало координатных осей x, y, z. Из прямоугольного треугольника ОАМ_i следует , где . И так как радиус-вектор точки : , то, проектируя это равенство на ось u, получим (, , - углы между осью u и осями x, y, z).

Рис. 14.3.

Как известно из тригонометрии .

Поэтому

И, группируя подобные члены, содержащие косинусы одинаковых углов, получим:

Но

где - расстояния от точки М_i до осей x, y, z, соответственно.

Поэтому

где I_x, I_y, I_z – моменты инерции тела относительно осей координат; I_xy, J_yz, J_xz - центробежные моменты инерции относительно осей отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется главной осью инерции. Например, если J_yz = 0 и J_xz = 0, то ось z – главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка О, от выбора начала координат, то обязательно надо указать для какой точки определены эти моменты инерции. Если начало координат взято в центре масс С, то все главные оси инерции называются главными центральными осями инерции.

Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (2) упрощается:

. (3)

Иногда по некоторым признакам нетрудно найти главные оси инерции тела.

1. Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось z по оси симметрии. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно отыскать точку с координатами (-x_i, -y_i, -z_i) и поэтому центробежные моменты инерции и . Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии.

2. Если у однородного тела имеется плоскость симметрии, то любая ось перпендикулярная ей будет главной осью инерции для всех точек этой плоскости.

Направим ось z перпендикулярно плоскости симметрии из любой её точки О, назначив там начало координат. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно найти симметричную ей точку с координатами (x_i, y_i, - z_i). Поэтому центробежные моменты инерции I_xz и I_yz будут равны нулю. Значит ось z – главная ось инерции.

Пример 5. Определим момент инерции диска относительно оси u, расположенной под углом γ к оси симметрии диска z (рис.8).

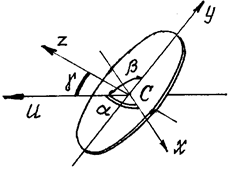
Рис.8

Решение. Оси x, y и z – главные центральные оси инерции, т.к. они являются осями симметрии.

Тогда , где - угол между осями u и z; угол - угол между осями u и y, равный ; угол - угол между осями u и x, равный 90°. Поэтому

Пример 6. На рисунке изображены однородные пластины, составленные из треугольных пластин (рис.8.1). Сравнить их моменты инерции относительно оси ОО₁.

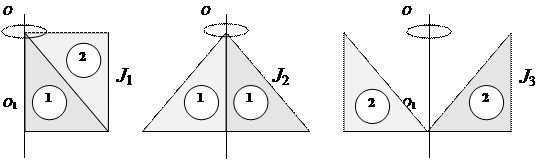
Рис.8.1

Решение. Рассмотрим треугольную пластину как систему материальных точек. Ее момент инерции по определению равен 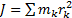, где m_k - массы материальных точек, r_k - расстояния от точек до оси вращения. Обратимся к первому рисунку (рис.8.1). Пластинки 1 и 2 имеют одинаковую площадь, поэтому можно постулировать, что они состоят из одинакового количества материальных точек. Видно, что у пластинки 2 материальные точки находятся дальше от оси вращения, чем у пластинки 1. Поэтому пластинка 2 обладает большим моментом инерции. На втором рисунке обе пластины обладают меньшим моментом инерции, а на третьем рисунке обе пластины обладают большим моментом инерции. Следовательно, J₁<J₁<J₃.

Уравнение динамики вращательного движения твердого тела.

Для того чтобы тело, закрепленное на оси, привести во вращение или изменить угловую скорость его вращения, к телу необходимо приложить силу . При вращении тела результат действия силы зависит не только от ее значения, но и от того, на каком расстоянии от оси вращения и под каким углом она приложена.

Моментом силы относительно неподвижной оси вращения называется векторное произведение радиус-вектора точки приложения силы на эту силу (рис.9):

Вектор направлен вдоль оси вращения в сторону, определяемую правилом правого винта (рис.10). Модуль момента силы определяется выражением:

где r∙sinα=h - плечо силы F; α – угол между и .

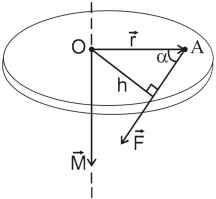
Рис.9

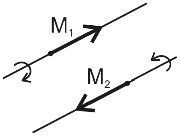
Рис. 10

Плечом силы h называют кратчайшее расстояние между линией действия силы и осью вращения (рис. 9). Таким образом, момент силы равен произведению силы на плечо этой силы:

M=F∙h [Н∙м].

Уравнение динамики вращательного движения твердого тела имеет вид

Момент действующих на тело сил равен произведению момента инерции тела на угловое ускорение.

Пример 7. Через блок, укрепленный на горизонтальной оси, проходящей через его центр, перекинута нить, к концам которой прикреплены грузы m₁=300 г и m₂=200 г (рис.11). Масса блока m₀=300 г. Блок считать однородным диском. Найти ускорение грузов a - ?

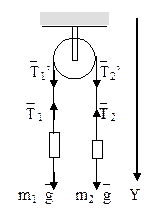
Рис.11

Решение. Второй закон Ньютона для первого груза

для второго груза:

Основное уравнение динамики вращательного движения для блока:

где и моменты сил натяжения и .

Так как нить нерастяжима, то:

a₁= a₂= a, a=𝜀∙r, (4)

а так как нить невесома: Т₁= и Т₂=.

Для перехода к скалярным соотношениям для описания движения грузов введем ось Y. Тогда a_1y=a, a_2y = –a. Тогда векторные уравнения (1) и (2) можно заменить скалярными

m₁a₁=m₁g-T₁, - m₂a₂=m₂g-T₂. (5)

Моменты сил и направлены по оси вращения, но в противоположные стороны. Примем направление вектора за положительное. Тогда векторное уравнение (3) можно переписать в виде

где r - радиус блока.

Очевидно, Т₁=Т₂, если масса блока, а следовательно, и его момент инерции пренебрежительно малы. Выражая из (4) ε и учитывая, что момент инерции однородного диска J=m₀r²/2, получаем

Уравнения (5) и (6) образуют систему. Сокращая в уравнении (6) радиус блока r и складывая все три уравнения [предварительно второе из уравнений (5) надо умножить на -1], получаем

Пример 8. Две гири с массами m₁=2 кг и m₂=1 кг соединены нитью и перекинуты через блок массой m_б=1 кг. Найти: 1) ускорение a - ?, с которым движутся гири; 2) натяжения нитей Т₁ - ? и Т₂ - ?, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.

Решение. Движение первой гири вниз происходит под действием двух сил: силы тяжести m₁g (направленного вниз) и натяжения нити Т₁ (направленного вверх). Поэтому для этой гири будем иметь:

m₁a=m₁g-T₁. (1)

Вторая гиря движется вверх с тем же ускорением а под действием силы тяжести m₂g (вниз) и натяжения нити Т₂ (вверх). Поэтому для нее:

m₂a=m₂g+T₂. (2)

Нить будет натянута по обе стороны блока по-разному, и разность ее натяжений Т₁ - Т₂ будет создавать момент, вращающий блок. Применяя основной закон динамики, получим:

где

1) Решая (1), (2), (3) и (4) совместно, найдем

2) Подставляя (5) в (1) и (2), получим соответственно

Пример 9. На барабан массой m_б=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение груза a-?. Барабан считать однородным цилиндром. Трением пренебречь.

Решение. Задачу можно решить двумя способами: 1) применяя основной закон динамики вращательного движения (см. решение предыдущего примера) и 2) применяя закон сохранения энергии. Решение задачи первым способом предлагается сделать самостоятельно. При решении задачи вторым способом рассуждаем так: при опускании груза его потенциальная энергия уменьшается, переходя в кинетическую энергию груза и в кинетическую энергию вращения барабана. Таким образом,

Но так как J=m_бR²/2 и 𝜔=v/R, где R - радиус барабана, то уравнение (1) можно написать так:

Так как опускание груза происходит под действием постоянной силы, то движение груза равноускоренное, поэтому

h=at²/2 и v=at. (3)

Подставим (3) в (2) и получим

Пример 10. Однородный цилиндр радиуса R раскрутили вокруг его оси до угловой скорости ω и поместили в угол (рис.11.1). Коэффициент трения между стенками угла и поверхностью цилиндра равен μ. Сколько оборотов сделает цилиндр до остановки?

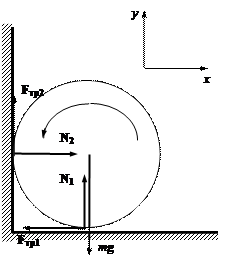
Рис.11.1

Решение. На вращающийся в углу цилиндр действуют: Земля с силой тяжести mg, горизонтальная поверхность с силами N₁ и F_тр1, а также вертикальная поверхность с силами N₂ и F_тр2, причем, силы трения являются силами трения скольжения, поэтому справедливы соотношения:

Применим основное уравнение динамики вращательного движения, согласно которому

Учитывая, что момент инерции сплошного цилиндра относительно оси, проходящей через центр масс, равен и вычисляя моменты указанных сил

получаем

Поскольку центр масс цилиндра неподвижен (a_c=0), векторная сумма действующих на него сил равна нулю, то есть

Спроектируем это выражение на оси координат:

Из уравнений (2) и (3) найдем N₁ и N₂:

Полученные выражения подставим в формулу (1)

откуда получаем выражение для углового ускорения

Решение “динамической” части задачи приводит к заключению, что вращение происходит с постоянным угловым ускорением. Следовательно, при решении кинематической части задачи можно воспользоваться законами движения в виде

К моменту остановки φ(t_ост)=2πN, где N - число оборотов, ω(t_ост)=0, поэтому

Выразив из последнего уравнения и подставив это значение в первое кинематическое уравнение, получим

Учитывая выражение для углового ускорения (4), находим число оборотов до остановки

Пример 11. К ободу однородного диска радиусом R = 0,2 м приложена касательная сила R = 100 Н. При вращении на диск действует момент сил трения M_тр=5 Н∙м. Определить массу диска, если он вращается с угловым ускорением ε=100 рад/с².

Решение. Момент инерции диска относительно оси, проходящей через его центр масс, равен

Момент сил, действующих на диск, равен

M=F∙R-M_тр.

Подставляя это в основное уравнение динамики вращательного движения , получим

Откуда

Пример 12. Тонкая однородная палочка длины l и массы m кладется на две опоры так, что точки опоры расположены у ее концов (рис.11.2). Одну из опор убирают. Найти силу реакции оставшейся опоры в первоначальный момент времени.

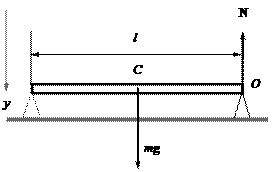
Рис.11.2

Решение. После того, как убрали одну из опор, палочка начала совершать вращательное движение вокруг оси О, и для описания вращения применяется основное уравнение динамики вращательного движения (действующие на палочку силы тяжести mg и реакции опоры N указаны на рис.11.5):

где - момент инерции стержня относительно оси О, проходящей через конец стержня; - момент силы тяжести относительно оси вращения О, момент силы N равен нулю.

В уравнение (1), как видим, не входит сила N, которую требуется найти. Запишем уравнение движения центра масс, в данном случае находящегося в середине палочки (точка С):

Учитывая, что в начальный момент времени скорость центра масс v_c=0 и, следовательно, нормальное ускорение a_n=0, приходим к выводу, что ускорение точки С равно тангенциальному и может быть выражено через угловое ускорение следующим образом:

В проекции на ось у уравнение движения центра масс приобретает вид

Откуда

Находим из уравнения (1) угловое ускорение

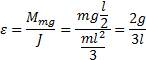
и, подставляя его в (3), получаем силу нормального давления в начальный момент движения

Пример 13. На рис.11.3 изображена катушка, на которую намотан тонкий слой ниток. Катушка находится на наклонной плоскости с углом α. Нить тянут с силой F, направленной под углом β к наклонной плоскости. Определить величину и указать направление момента каждой силы, действующей на катушку.

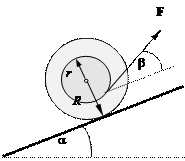
Рис.11.3

Решение. Изобразим силы, действующие на катушку (рис.11.4). Это сила тяжести mg как проявление действия гравитационного поля Земли, силы нормального давления N и трения F_тр, возникающие при контакте катушки с наклонной плоскостью, а также сила F, действующая со стороны нити.

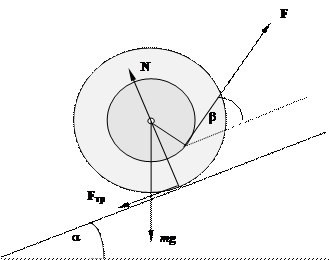
Рис.11.4

Согласно определению момента силы относительно оси вращения, величина момента силы равна произведению силы на плечо. Две силы - сила тяжести и нормального давления, проходят через ось вращения, их моменты равны нулю: M_mg=0, M_N=0. Плечом силы F является радиус окружности слоя ниток r, момент этой силы M_F=F∙r. Плечом силы трения F_тр является радиус катушки R, момент этой силы . Направление момента силы находится по правилу векторного произведения M=[r, F], которое можно интерпретировать как правило буравчика или правило правого винта. Если головку винта расположить в плоскости, построенной через векторы r и F, и вращать его от первого вектора в векторном произведении ко второму, то поступательное движение винта укажет направление вектора момента силы М. Таким образом, момент силы трения направлен перпендикулярно плоскости рисунка “от нас”, а момент силы со стороны нити - “к нам”.

Пример 14. Два цилиндра с равными высотами и равными массами вращаются относительно своих осей. Плотности материалов цилиндра ρ₁>ρ₂. Сравнить вращающие моменты, если угловые ускорения цилиндров одинаковы.

Решение. Поскольку плотность материала первого цилиндра больше, чем второго, его объем должен быть меньше. Соответственно радиус первого цилиндра меньше, чем второго R₁<R₂. Момент инерции цилиндра рассчитывается по формуле , из чего следует, что J₁<J₂. Согласно основному закону динамики вращательного движения вращающий момент M=J∙ε. При одинаковых угловых ускорениях момент силы больше для тела с большим моментом инерции, то есть M₂<M₁.

Пример 15. На рис.11.5 изображен график зависимости угловой скорости вращающегося тела. Как изменяется величина вращающего момента на участках “а” и “б”?

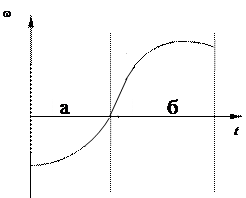
Рис.11.5

Решение. Применяя формулу ε=dω/dt, определим характер изменения углового ускорения в указанные интервалы времени. Затем применим уравнение динамики вращательного движения M=J∙ε.

В интервале “а” наклон кривой, а следовательно и производная dω/dt возрастает, соответственно увеличиваются угловое ускорение и вращающий момент.

В интервале “б” наклон кривой, а следовательно и производная dω/dt уменьшается, что приводит к уменьшению вращающего момента.

Дифференциальные уравнения движения системы.

Рассмотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой . Обозначим равнодействующую всех приложенных к точке внешних сил (и активных и реакций связей) через , а равнодействующую всех внутренних сил – через . Если точка имеет при этом ускорение , то по основному закону динамики

.

Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

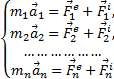
Эти уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме. Уравнения являются дифференциальными, так как ; входящие в правые части уравнений силы будут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя на какие-нибудь координатные оси, мы можем получить дифференциальные уравнения движения системы в проекциях на эти оси.

Полное решение основной задачи динамики для системы состояло бы в том, чтобы, зная заданные силы, проинтегрировать соответствующие дифференциальные уравнения и определить таким путем закон движения каждой из точек системы в отдельности.

Однако такой путь решения обычно не применяется по двум причинам. Во-первых, этот путь слишком сложен и почти всегда связан с непреодолимыми математическими трудностями. Во-вторых, в большинстве случаев при решении задач механики бывает достаточно знать некоторые суммарные характеристики движения системы в целом, а не движение каждой из ее точек в отдельности. Эти суммарные характеристики определяются с помощью общих теорем динамики системы, к изучению которых мы и перейдем.

Основная роль уравнений состоит в том, что они, или следствия из них, являются исходными для получения соответствующих общих теорем.

Общие теоремы динамики механической системы: теоремы о движении центра масс механической системы и об изменении количества движения, теоремы об изменении кинетического момента и кинетической энергии, являются следствием основного уравнения динамики. Данные теоремы рассматривают не движение отдельных точек и тел, входящих в механическую систему, а некоторые интегральные характеристики, такие как движение центра масс механической системы, ее количество движения, кинетический момент и кинетическую энергию. В результате из рассмотрения исключаются неизвестные внутренние силы, а в ряде случаев и реакции связей, что существенно упрощает решения задачи.

Теорема о движении центра масс.

В ряде случаев для определения характера движения системы (особенно твердого тела), достаточно знать закон движения ее центра масс. Например, если бросить камень в цель, совсем не нужно знать как он будет кувыркаться во время полета, важно установить попадет он в цель или нет. Для этого достаточно рассмотреть движение какой-нибудь точки этого тела.

Чтобы найти этот закон, обратимся к уравнениям движения системы и сложим почленно их левые и правые части. Тогда получим:

Преобразуем левую часть равенства. Из формулы для радиус-вектора центра масс имеем:

Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производных, найдем:

или

где - ускорение центра масс системы. Так как по свойству внутренних сил системы , то, подставляя все найденные значения, получим окончательно:

Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением движения материальной точки, получаем другое выражение теоремы: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Проектируя обе части равенства на координатные оси, получим:

Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.

Значение доказанной теоремы состоит в следующем.

1) Теорема дает обоснование методам динамики точки. Из уравнений видно, что решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т.е. имеют вполне конкретный смысл.

В частности, если тело движется поступательно, то его движение полностью определяется движением центра масс. Таким образом, поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс.

2) Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все наперед неизвестные внутренние силы. В этом состоит ее практическая ценность.

Так движение автомобиля по горизонтальной плоскости может происходить только под действием внешних сил, сил трения, действующих на колеса со стороны дороги. И торможение автомобиля тоже возможно только этими силами, а не трением между тормозными колодками и тормозным барабаном. Если дорога гладкая, то как бы не затормаживали колеса, они будут скользить и не остановят автомобиль.

Или после взрыва летящего снаряда (под действием внутренних сил) части, осколки его, разлетятся так, что центр масс их будет двигаться по прежней траектории.

Теоремой о движении центра масс механической системы следует пользоваться для решения задач механики, в которых требуется:

- по силам, приложенным к механической системе (чаще всего к твердому телу), определить закон движения центра масс;

- по заданному закону движения тел, входящих в механическую систему, найти реакции внешних связей;

- по заданному взаимному движению тел, входящих в механическую систему, определить закон движения этих тел относительно некоторой неподвижной системы отсчета.

С помощью этой теоремы можно составить одно из уравнений движения механической системы с несколькими степенями свободы.

При решении задач часто используются следствия из теоремы о движении центра масс механической системы.

Следствие 1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Так как ускорение центра масс равно нулю, .

Следствие 2. Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.

Например, если на тело начнут действовать две силы, образующие пару сил (рис.12), то центр масс С его будет двигаться по прежней траектории. А само тело будет вращаться вокруг центра масс. И неважно, где приложена пара сил.

Кстати, в статике мы доказывали, что действие пары на тело не зависит от того, где она приложена. Здесь мы показали, что вращение тела будет вокруг центральной оси С.

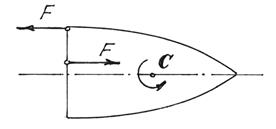
Рис.12

Пример 16. Человек перешел с кормы лодки на нос. Определим перемещение лодки s (рис.13). Вес лодки – Р₁, человека – Р₂, длина лодки – l. Сопротивление движению не учитываем.

Решение. Определим движение центра масс С системы, состоящей из человека и лодки.

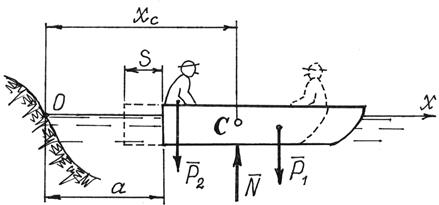
Рис.13

Составляем дифференциальное уравнение движения центра масс по оси х: . Но так как проекции внешних сил , и на ось х равны нулю, то . Проинтегрировав дважды это уравнение, получим и . Но в начале движения система была неподвижна Значит, .

Найдем координату в первом положении системы, когда человек находился на корме, как координату центра тяжести:

И во втором положении, когда человек перейдет на нос лодки:

Приравниваем координаты, т.к. ,

Из этого равенства находим перемещение лодки

Пример 17. Рассмотрим систему, которая состоит из однородного стержня ОА и кольца М. Стержень длины L и массы вращается вокруг горизонтальной оси, проходящей через точку О (рис.14). Кольцо массы m может без трения скользить по стержню. К нему прикреплена пружина, коэффициент жесткости которой равен С. Положение кольца на стержне определяется координатой . Определим проекции реакции опоры О на оси неподвижной декартовой системы координат Oxy.

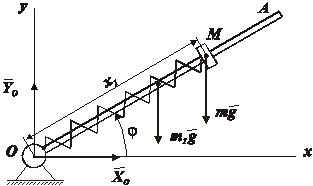
Рис.14

Решение. Запишем уравнение теоремы о движении центра масс для рассматриваемой механической системы в векторном виде.

Силы взаимодействия кольца со стержнем и пружиной есть внутренние силы системы, поэтому в уравнении они в явном виде не присутствуют. Проектируя уравнение (5) на оси системы координат Oxy, получаем

По формулам (1) находим координаты центра масс системы

затем, дифференцируя (7), запишем

и, наконец, вычисляя вторые производные, получим

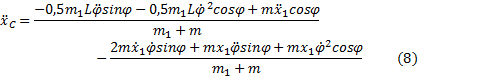
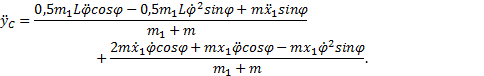
Подставляя (8) в уравнения (6), получаем проекции реакции в опоре O на оси неподвижной системы координат:

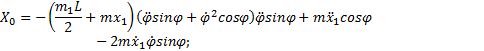
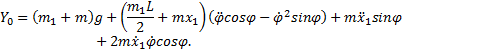
Если в полученные уравнения подставить значения обобщенных координат и ускорений для какого-либо момента времени, можно найти величины искомых проекций.

Пример 18. Механизм шарнирного параллелограмма состоит из двух кривошипов О₁А и O₂В, а также шатуна АВ, имеющих массу т и длину l каждый (рис.14.1). Кривошипы вращаются с постоянной угловой скоростью ω. Определить сумму горизонтальных составляющих реакций шарниров О₁ и O₂ в функции угла ψ.

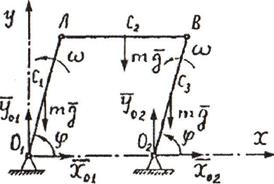
Рис.14.1

Решение. Система состоит из трех подвижных тел, два из которых двигаются вращательно, а одно - поступательно. На систему тел действуют внешние силы: тяжести mg, также составляющие реакций неподвижных шарниров

По теореме о движении центра масс системы в проекции на ось Ох

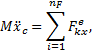
где М=3т и F_kx = Х₀₁ + Х₀₂.

Горизонтальная координата центра масс равна:

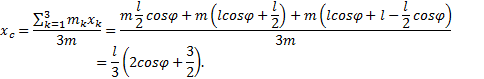
Дифференцируя это выражение по времени t (с учетом ψ = ωt) получим

Сумма проекций горизонтальных составляющих реакций шарниров равна:

Теорема об изменении кинетического момента.

Кинетический момент механической системы относительно неподвижного центра O является мерой движения системы вокруг этого центра. При решении задач обычно применятся не сам вектор , а его проекции на оси неподвижной системы координат, которые называются кинетическими моментами относительно оси. Например, K_z - кинетический момент системы относительно неподвижной оси Oz .

Кинетический момент механической системы складывается из кинетических моментов точек и тел, входящих в эту систему. Рассмотрим способы определения кинетического момента материальной точки и твердого тела при различных случаях их движения.

Для материальной точки с массой , имеющей скорость , кинетический момент относительно некоторой оси Oz определяется как момент вектора количества движения этой точки относительно выбранной оси:

Кинетический момент точки считается положительным, если со стороны положительного направления оси движение точки происходит против часовой стрелки.

Если точка совершает сложное движение, для определения ее кинетического момента следует вектор количества движения рассматривать как сумму количеств относительного и переносного движений (рис.15)

Тогда

Но , где - расстояние от точки до оси вращения, и

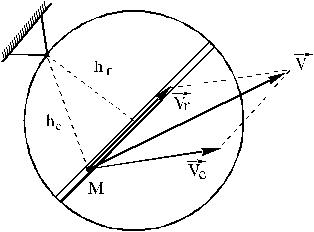
Рис. 15

Вторую составляющую вектора кинетического момента можно определить так же, как и момент силы относительно оси. Как и для момента силы, величина равна нулю, если вектор относительной скорости лежит в одной плоскости с осью переносного вращения.

Кинетический момент твердого тела относительно неподвижного центра можно определить как сумму двух составляющих: первая из них характеризует поступательную часть движения тела вместе с его центром масс, вторая - движение системы вокруг центра масс:

.

Если тело совершает поступательное движение, то вторая составляющая равна нулю

.

Наиболее просто вычисляется кинетической момент твердого тела при его вращении вокруг неподвижной оси

,

где - момент инерции тела относительно оси вращения.

Теорема об изменении кинетического момента механической системы при ее движении вокруг неподвижного центра формулируется следующим образом: полная производная по времени от вектора кинетического момента механической системы относительно некоторого неподвижного центра O по величине и направлению равна главному моменту внешних сил, приложенных к механической системе, определенному относительно того же центра

где - главный момент всех внешних сил относительно центра О.

При решении задач, в которых рассматриваются тела, вращающиеся вокруг неподвижной оси, используют теорему об изменении кинетического момента относительно неподвижной оси

Как и для теоремы о движении центра масс, теорема об изменении кинетического момента имеет следствия.

Следствие 1. Если главный момент всех внешних сил относительно некоторого неподвижного центра равен нулю, то кинетический момент механической системы относительно этого центра остается неизменным.

Следствие 2. Если главный момент всех внешних сил относительно некоторой неподвижной оси равен нулю, то кинетический момент механической системы относительно этой оси остается неизменным.

Теорема об изменении кинетического момента применяется для решения задач, в которых рассматривается движение механической системы, состоящей из центрального тела, вращающегося вокруг неподвижной оси, и одного или нескольких тел, движение которых связано с центральным.. Связь может осуществляться при помощи нитей, тела могут перемещаться по поверхности центрального тела или в его каналах за счет внутренних сил. С помощью данной теоремы можно определить зависимость закона вращения центрального тела от положения или движения остальных тел.

Пример 19. Рассмотрим применение теоремы об изменении кинетического момента для определения внешнего момента, обеспечивающего равномерное движение ведущего звена механической системы. Механическая система (рис.16) состоит из однородной трубки CD длиной L, массы , образующей с осью вращения прямой угол и шарика массы m.

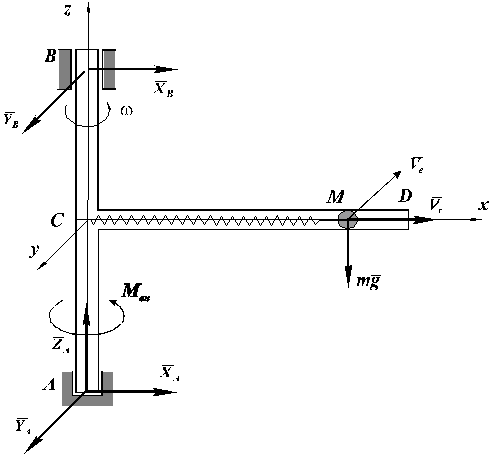
Рис.16

Решение. В момент времени t=0 под действием внешнего момента M_вр трубка начинает вращаться вокруг вертикальной оси с постоянной угловой скоростью . Необходимо определить, каким должен быть этот момент, чтобы сохранялась постоянная угловая скорость вращения трубки CD. При решении пренебречь трением, массой стержня АВ и пружины.

Применим теорему об изменении кинетического момента, выбрав за ось z ось вращения АВ,

. (9)

Определим кинетический момент рассматриваемой системы относительно оси Az. Трубка (однородный прямолинейный стержень) совершает вращение вокруг оси, перпендикулярной стержню и проходящей через его конец, имеет кинетический момент

,

где - осевой момент инерции трубки,

- угловая скорость вращения.

Шарик М совершает сложное движение - относительное вдоль трубки со скоростью и переносное вместе с трубкой. Переносная скорость перпендикулярна трубке и по модулю равна . При определении переносной скорости за начало отсчета координаты x принята точка С трубки, лежащая на оси вращения. Кинетический момент шарика относительно оси z равен , т.к. вектор пересекает ось z и его момент относительно этой оси равен нулю.

Кинетический момент всей системы равен

. (10)

Определим главный момент внешних сил относительно оси z. Силы тяжести трубки и шарика параллельны оси вращения и момента относительно этой оси не создают. Реакции опор пересекают ось вращения и момент этих сил относительно оси z также равен нулю. Силы динамического взаимодействия между шариком и трубкой, включая упругую силу пружины F_упр, есть силы внутренние. Поэтому

, (11)

где - внешний момент, обеспечивающий равномерное вращение трубки.

Подставляя (8) и (9) в уравнение теоремы об изменении кинетического момента системы (7), получаем:

откуда следует, что искомый внешний момент, обеспечивающий равномерное вращение трубки должен быть равен

.

Если в полученное соотношение подставить численные значения координаты x и относительной скорости , которые были получены в первом разделе курсовой работы, можно найти значение вращающего момента для любого момента времени и построить график изменения на исследуемом интервале времени.

Пример 20. Тонкий однородный стержень массы m и длиной ОА=l может вращаться без трения вокруг горизонтальной оси О. В начальный момент времени стержень отведен в горизонтальное положение и отпущен без начальной скорости. Определить угловую скорость и угловое ускорение стержня, когда он повернется на угол α.

Решение. По теореме об изменении кинетического момента системы составим дифференциальное уравнение вращательного движения стержня вокруг оси О

Учитывая, что момент инерции стержня равен

Получим

Воспользуемся подстановкой

Разделим переменные и проинтегрируем исходное дифференциальное уравнение вращательного движения стержня с учетом начальных условий движения (при φ = 0, ω₀ = 0)

Угловая скорость стержня

Пример 21. Груз массой m подвешен на тросе, навитом на барабан массой m₁ с горизонтальной осью вращения. Пренебрегая потерями на трение и считая барабан сплошным однородным цилиндром, определить ускорение груза.

Рис.17

Решение. На систему тел действуют внешние силы: m₁g, mg, а также реакции подшипников и .

На основании теоремы об изменении кинетического момента имеем

Кинетический момент системы относительно оси вращения барабана

где (v - скорость груза; R - радиус барабана).

Далее получим

Ускорение груза

Пример 22. Через блок массой m₁= 0,2т, имеющего горизонтальную ось вращения, переброшена веревка, к одному концу которой подвешен груз массой т, а за другой конец ухватился человек, имеющий ту же массу т. Пренебрегая массой веревки и считая массу блока равномерно распределенной по его ободу, определить скорость груза, если человек начнет подниматься по веревке с относительной скоростью и.

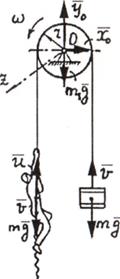
Рис.18

Решение. На систему тел действуют внешние силы: mg, m₁g, а также реакции подшипников и .

На основании теоремы об изменении кинетического момента имеем

В данном случае выполняется закон сохранения кинетического момента системы относительно оси. Составим уравнение

или

где - угловая скорость блока

Скорость груза

Пример 23. Для экспериментального определения момента трения в подшипниковых опорах на вал насажен маховик массы M = 500 кг (рис. 19); радиус инерции маховика ρ=1,5 м. Маховику сообщена угловая скорость, соответствующая частоте вращения n = 240 об/мин; предоставленный самому себе, он остановился через 10 мин. Определить момент трения M_T, считая его постоянным.

Рис.19

Решение. Вычислим угловую скорость вращения вала в начальный момент времени и момент инерции маховика относительно оси вращения:

Уравнение динамики маховика, согласно теоремы об изменении кинетического момента

и с учетом 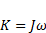, имеет вид

Проинтегрируем это уравнение по времени t

где C – постоянная интегрирования, значение которой, в соответствии с начальным условием ω(0)=ω₀, равно ω₀. Так как через T = 600 с маховик остановился, то

Откуда

Пример 24. На вращающейся платформе стоит человек с вытянутыми в стороны руками. Платформе сообщается угловая скорость, соответствующая частоте вращения n₀ =15 об/мин. При этом момент инерции человека и платформы относительно оси вращения J₀ = 0,8 кг∙м². С какой угловой скоростью начнет вращаться платформа с человеком, если, приблизив руки к туловищу, он уменьшит момент инерции системы до 0,12 кг∙м²? Трением пренебречь.

Решение. Определим угловую скорость системы в начальный момент времени:

Проанализируем силы, действующие на систему. На человека и платформу действуют только силы тяжести, которые направлены вдоль оси вращения и, следовательно, моменты сил тяжести относительно этой оси равны нулю. Таким образом, уравнение теоремы об изменении кинетического момента

будет иметь вид

где Z – ось вращения.

Первый интеграл этого уравнения K_z=const, т.е. кинетический момент системы относительно оси Z не изменяется. Из этого следует

и

что соответствует частоте вращения

Закон сохранения движения центра масс.

Из теоремы о движении центра масс можно получить следующие важные следствия:

1) Пусть сумма внешних сил, действующих на систему, равна нулю

.

Тогда из уравнения следует, что или . Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т. е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Действие внутренних сил, как мы видим, движение центра масс системы изменить не может.

2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось Ох) равна нулю:

.

Тогда уравнение дает: или .

Следовательно, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент , то и в любой последующий момент , т.е. центр масс системы в этом случае вдоль оси Ох перемещаться не будет ().

Все эти результаты выражают собою закон сохранения движения центра масс системы. Рассмотрим некоторые примеры, иллюстрирующие его приложения.

а) Движение центра масс солнечной системы. Так как притяжением звезд можно практически пренебречь, то можно считать, что на солнечную систему никакие внешние силы не действуют. Следовательно, в первом приближении ее центр масс движется в мировом пространстве равномерно и прямолинейно.

б) Действие пары сил на тело. Если на свободное твердое тело начнет действовать пара сил , то геометрическая сумма этих внешних сил будет равна нулю . Следовательно, центр масс С тела, если он вначале был неподвижен, должен остаться неподвижным и при действии пары. Таким образом, где бы к свободному твердому телу ни была приложена пара сил, тело начнет вращаться вокруг своего центра масс.

в) Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий (силы внутренние) не мог бы двигаться вдоль горизонтальной плоскости, так как в этом случае сумма проекций на любую горизонтальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет ().

Если, например, человек вынесет правую ногу вперед, то левая его нога скользнет назад, а общий центр масс останется на месте.

При наличии же трения скольжению левой ноги назад будет препятствовать сила трения, которая в этом случае будет направлена вперед. Эта сила и будет той внешней силой, которая позволяет человеку перемещаться в сторону ее действия (в данном случае вперед).

Аналогично происходит движение паровоза или автомобиля. Сила давления пара или газа в двигателе является силой внутренней и сама но себе не может переместить центр масс системы. Движение происходит потому, что двигатель передает соответствующим колесам, называемыми ведущими, вращающий момент. При этом точка касания В ведущего колеса (рис.20) стремится скользить влево. Тогда на колесо будет действовать сила трения, направленная вправо. Эта внешняя сила и позволит центру тяжести паровоза или автомобиля двигаться вправо. Когда этой силы нет или когда она недостаточна для преодоления сопротивления, испытываемого ведомыми колесами, движения вправо не будет; ведущие колеса будут при этом вращаться на месте (буксовать).

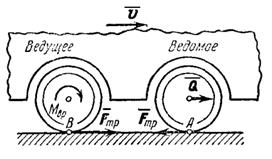
Рис.20

Вопросы для самопроверки

- Что такое масса системы?

- Что называют центром масс системы точек и как определяют его координаты?

- Дайте определение внешним и внутренним силам, действующим на систему.

- Какими свойствами обладают внутренние силы?

- Может ли центр масс твердого тела находиться вне этого тела?

- Запишите формулы для вычисления координат центра масс в трехмерном пространстве.

- Приведите определения статического момента системы материальных точек относительно: а) заданной точки; б) координатных плоскостей.

- Что называется полярным моментом инерции тела?

- Приведите определение осевого момента инерции системы материальных точек.

- Что называют центробежным моментом инерции тела? Напишите их выражения.

- Применим ли метод отрицательных весов для вычисления моментов инерции твердого тела?

- Как вычисляются моменты инерции тела относительно параллельных осей (теорема Штейнера)?

- Как классифицируют в динамике силы, действующие на точки механической системы?

- Что называют моментом инерции твердого тела относительно плоскости, оси и точки?

- Какую величину называют радиусом инерции тела относительно оси?

- Какова зависимость между моментами инерции, а также между радиусами инерции тела относительно параллельных осей?

- Моменты инерции каких тел вы знаете? Напишите формулы для их вычисления.

- Что представляет собой эллипсоид инерции и какие оси называют главными осями инерции твердого тела в данной точке?

- При каких условиях некоторая ось является главной осью инерции в данной точке?

- Как определить по эллипсоиду инерции, относительно какой оси из всех осей, проходящих через данную точку, момент инерции имеет наибольшее значение?

- Какими свойствами обладают главные и главные центральные оси инерции?

- Как вычисляют момент инерции твердого тела относительно произвольной оси, проходящей или не проходящей через центр масс тела?

- Относительно какого полюса момент инерции данного тела имеет наименьшее значение?

- Что называют тензором инерции тела в данной точке и что он характеризует?

- Из какого физического закона вытекает, что равнодействующая внутренних сил системы равна нулю?

- Приведите формулировку теоремы о движении центра масс механической системы.

- В каких случаях центр масс системы движется равномерно и прямолинейно?

- Запишите математическое выражение теоремы о движении центра масс в координатной форме.

- Сформулируйте теорему о движении центра масс системы?

- Какое движение твердого тела можно рассматривать как движение материальной точки, имеющей массу данного тела, и почему?

- При каких условиях центр масс системы находится в состоянии покоя и при каких условиях он движется равномерно и прямолинейно?

- При каких условиях центра масс системы не перемещается вдоль некоторой оси?

- Приведите примеры, иллюстрирующие теорему о движении центра масс механической системы.

- Какое действие на свободное твердое тело оказывает приложенная к нему пара сил?

Рисунок 23

- Тело массой 10 кг поднято на высоту 6 м. Определите потенциальную энергию тела и работу, которую совершит тело при падении с этой высоты?

- Материальная точка массой 16 кг, движущаяся со скоростью 10 м/с, остановилась через 40 с. Определите величину тормозной силы?

- Тело массой 9,2 кг двигалось из состояния покоя 3 сек с ускорением 4 м/с под действием силы F. Определите запас кинетической энергии, накопленный телом?

- Понятие внутренних сил:

1) силы, действующие на замкнутую систему

2) силы трения

3) силы гравитации

4) силы, действующие в замкнутой системе

5) кулоновские силы

- Момент инерции шара:

1)

2)

3)

4)

5)

- Математическое выражение теоремы Штейнера:

1)

2)

3)

4)

5)

- Какое выражение является основным уравнением динамики вращательного движения

1)

2)

3)

4)

5)

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00