Тема 7. Приведение сил к заданному центру
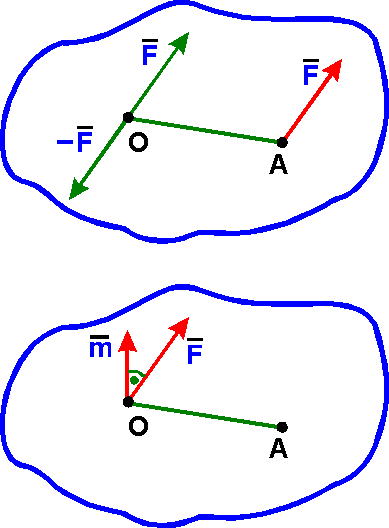 Теорема
о параллельном переносе силы: силу
F, не
изменяя ее действие на абсолютно твердое тело, можно
переносить из данной точки (А) в любую
другую точку (О) тела, прибавляя при
этом пару с моментом (m), равным моменту переносимой силы
относительно точки (О), куда сила
переносится [m = mo
(F)];
Теорема
о параллельном переносе силы: силу
F, не
изменяя ее действие на абсолютно твердое тело, можно
переносить из данной точки (А) в любую
другую точку (О) тела, прибавляя при
этом пару с моментом (m), равным моменту переносимой силы
относительно точки (О), куда сила
переносится [m = mo
(F)];
{F} ~ {F, m}.
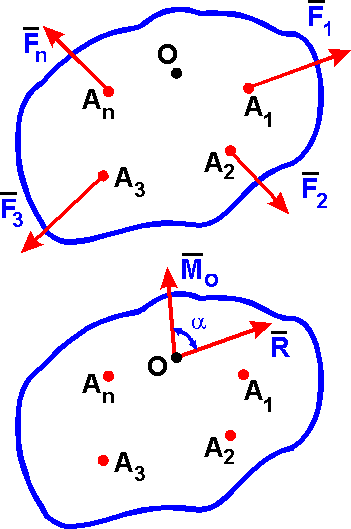 Задача о приведении
системы сил F1, F2, ..., Fn к произвольном центру (точке) О, т. е.
замене данной системы сил другой эквивалентной
более простой, решается применением теоремы
Пуансо: любая система сил F1, F2, ..., Fn
действующих на абсолютно твердое тело, при
приведении к произвольному центру О заменяется одной силой R,
равной главному вектору системы сил, приложенной
в центре О и парой сил с моментом Mo, равным главному моменту системы сил
относительно центра (точки) О. Главный
вектор
Задача о приведении
системы сил F1, F2, ..., Fn к произвольном центру (точке) О, т. е.
замене данной системы сил другой эквивалентной
более простой, решается применением теоремы
Пуансо: любая система сил F1, F2, ..., Fn
действующих на абсолютно твердое тело, при
приведении к произвольному центру О заменяется одной силой R,
равной главному вектору системы сил, приложенной
в центре О и парой сил с моментом Mo, равным главному моменту системы сил
относительно центра (точки) О. Главный
вектор
R = F1 + F2 + ... + Fn = SFk, (k = 1,
2, ..., n) |
а главный момент системы сил
относительно центра (точки) О
Mo = m1 + m2 + ... + mn =
= mo(F1) + mo(F2) + ... + mo(Fn) = Smo(Fk). (k = 1, 2, ..., n) |
Величина главного вектора
R не зависит от
выбора центра О, а значение главного момента
Mo при изменении положения центра О
может в общем случае изменяться.
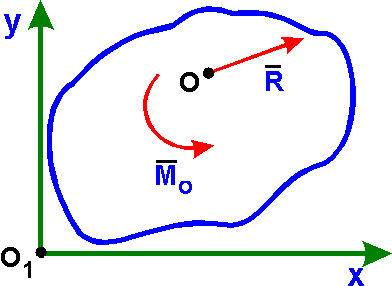 Для плоской системы
сил F1, F2, ..., Fn главный вектор R лежит в плоскости действия сил, а главный
момент перпендикулярен этой плоскости (a = 90°). Поэтому
главный момент плоской системы сил относительно
центра О определяется как сумма
алгебраических моментов сил относительно точки
(центра) О
Для плоской системы
сил F1, F2, ..., Fn главный вектор R лежит в плоскости действия сил, а главный
момент перпендикулярен этой плоскости (a = 90°). Поэтому
главный момент плоской системы сил относительно
центра О определяется как сумма
алгебраических моментов сил относительно точки
(центра) О
Mo = Smo(Fk), (k = 1, 2, ..., n)
и изображается на плоскости дуговой
стрелкой.
При приведении
плоской системы сил возможны следующие случаи:
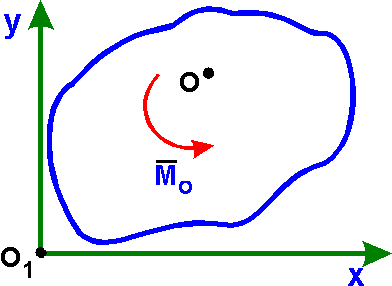 1. R = 0, Mo № 0:
1. R = 0, Mo № 0:
- система сил приводится к одной паре,
лежащей в плоскости действия сил, с моментом Mo.
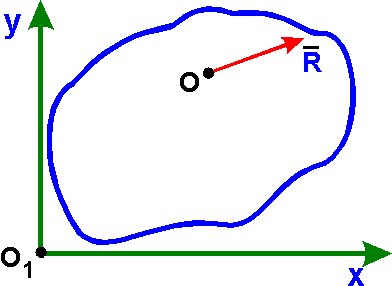 2. R № 0, Mo = 0:
2. R № 0, Mo = 0:
- система сил приводится к
равнодействующей R, приложеной
в точке О.
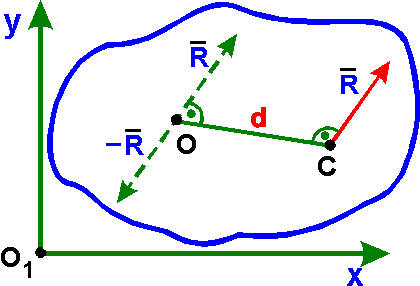 3. R № 0, Mo № 0:
3. R № 0, Mo № 0:
- система сил приводится к
равнодействующей R, проходящей через точку С,положение
которой определяется равенством
ОС = d = |
Mo |/R,
ОС ^ R. |
3. R
= 0, Mo = 0:
- уравновешенная
система сил:
для равновесия
плоской системы сил необходимо и достаточно,
чтобы главный вектор этой системы сил и ее
главный момент относительно любой точки были
равны нулю. |
 Теорема
о параллельном переносе силы: силу
F, не
изменяя ее действие на абсолютно твердое тело, можно
переносить из данной точки (А) в любую
другую точку (О) тела, прибавляя при
этом пару с моментом (m), равным моменту переносимой силы
относительно точки (О), куда сила
переносится [m = mo
(F)];
Теорема
о параллельном переносе силы: силу
F, не
изменяя ее действие на абсолютно твердое тело, можно
переносить из данной точки (А) в любую
другую точку (О) тела, прибавляя при
этом пару с моментом (m), равным моменту переносимой силы
относительно точки (О), куда сила
переносится [m = mo
(F)]; Задача о приведении
системы сил F1, F2, ..., Fn к произвольном центру (точке) О, т. е.
замене данной системы сил другой эквивалентной
более простой, решается применением
Задача о приведении
системы сил F1, F2, ..., Fn к произвольном центру (точке) О, т. е.
замене данной системы сил другой эквивалентной
более простой, решается применением  Для плоской системы
сил F1, F2, ..., Fn главный вектор R лежит в плоскости действия сил, а главный
момент перпендикулярен этой плоскости (a = 90°). Поэтому
главный момент плоской системы сил относительно
центра О определяется как сумма
алгебраических моментов сил относительно точки
(центра) О
Для плоской системы
сил F1, F2, ..., Fn главный вектор R лежит в плоскости действия сил, а главный
момент перпендикулярен этой плоскости (a = 90°). Поэтому
главный момент плоской системы сил относительно
центра О определяется как сумма
алгебраических моментов сил относительно точки
(центра) О 1. R = 0, Mo № 0:
1. R = 0, Mo № 0: 2. R № 0, Mo = 0:
2. R № 0, Mo = 0: 3. R № 0, Mo № 0:
3. R № 0, Mo № 0: