Тема 6. Теория пар сил, их свойства

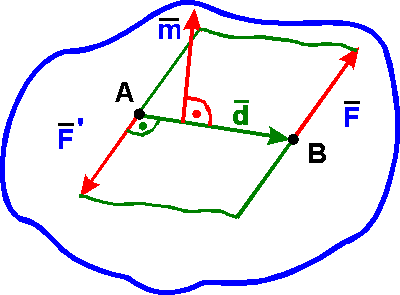    Система двух равных по модулю, параллельных и направленных в противоположные стороны сил называется парой сил (F = - Fў). Плоскость, в которой лежат силы F и Fў, называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил  - плечом пары.

    Пара сил не имеет равнодействующей, так как

R = F + Fў = 0.

    Действие пары сил F, Fў на абсолютно твердое тело сводится к вращательному эффекту, который характеризуется моментом пары.

    Моментом пары называется вектор

модуль которого равен произведению модуля одной из сил пары на ее плечо.

| m | = | F |Ч| d |.

    Вектор m направлен ^ плоскости пары в ту сторону, откуда пара видна стремящейся повернуть тело против часовой стрелки. Момент пары m - вектор свободный, т. е. его можно прикладывать в любой точке тела.

    Свойства момента пары:

    1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О:

m_o = m_o(F) + m_o(Fў).

    2. Момент пары равен моменту одной из сил пары относительно точки приложения другой силы пары:

m = m_А(F).

    Теорема 1. Пары сил с равными моментами эквивалентны.

    Следствия:

   1. Пару сил, приложенную к твердому телу, можно заменить другой парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:

m₁ = d₁ґF₁ = m₂ = d₂ґF₂

или

d₁ґF₁ = d₂ґF₂.

    2. Пару сил можно переносить в плоскость, параллельную плоскости пары.

    Теорема 2. Совокупность нескольких пар с моментами m₁, m₂, ..., m_n эквивалентна одной паре, момент m которой равен геометрической сумме моментов данных пар:

m = m₁ + m₂ + ... + m_n.

    Для пар, лежащих в одной плоскости, пользуются понятием алгебраического момента пары. Алгебраический момент пары равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары:

m = ± FЧd.

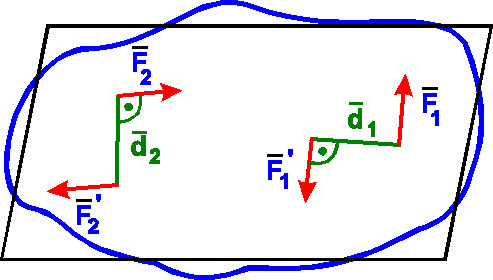
Знак плюс соответствует повороту тела под действием пары против хода часовой стрелки, минус - по ходу часовой стрелки:

m₁ = F₁Чd₁,    m₂ = - F₂Чd₂.

    Так как пара сил характеризуется только моментом, то пара сил, лежащая в плоскости, часто изображается только дуговой стрелкой (m₁, m₂), показывающей направление поворота пары.

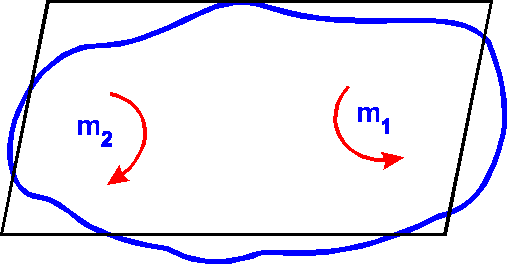
    Согласно теореме 2 о сложении пар на плоскости с моментами m₁, m₂, ..., m_n можно заменить одной парой, момент которой m равен алгебраической сумме моментов пар:

m = m₁ + m₂ + ... + m_n.