Система сил, линии действия которых лежат в одной плоскости называется плоской.

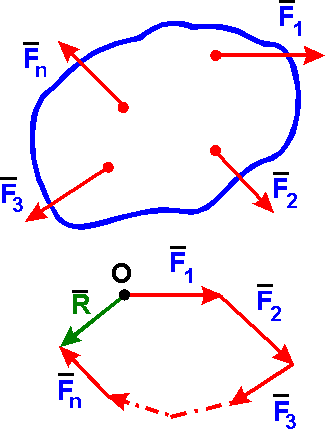
    Геометрический способ сложения сил. Геометрическая сумма (главный вектор) системы сил F₁, F₂, ..., F_n определяется построением силового многоугольника. Для этого пользуются правилом сложения векторов. В произвольной точке О вектор R, соединяющий начало первого вектора F₁ с концом последнего F_n изображает геометрическую сумму или главный вектор слагаемых сил:

R = F₁ + F₂ + ... + F_n = SF_k.     (k = 1, 2, .., n)

   Проекция силы на ось

    Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси:

F_х > 0, если 0 < a < p/2;

F_х < 0, если p/2 < a < p;

F_х = 0, если  a = p/2.

    Аналитический способ задания сил на плоскости

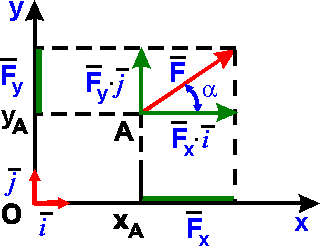
    Силу F на плоскости Оxy можно задать через ее проекции F_х и F_у на оси прямоугольной системы координат по правилу сложения векторов, определив точку А (x_A, y_A) приложения силы:

F  = F_хЧi + F_уЧj,

где i, j - единичные векторы. Модуль силы F и углы, которые она образует с координатными осями вычисляются по формулам:

     Аналитический способ сложения сил

    Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство R = SF_k на оси прямоугольной системы координат Оху, получим

где F_kx, F_ky - проекции k-ой силы F_k на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор R равные геометрической сумме слагаемых сил F₁, F₂, ..., F_n определяется по формулам: