Главная

Лекция 1. Введение. Основные понятия статики.

В данной лекции рассматриваются следующие вопросы

1. Введение.

2. Элементы векторной алгебры.

3. Основные понятия статики.

4. Аксиомы статики.

5. Связи и их реакции.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

Введение

Развитие современной техники ставит перед инженерами самые разнообразные задачи, связанные с расчетом различных сооружений (зданий, мостов, каналов, плотин и т. п.), с проектированием, производством и эксплуатацией всевозможных машин, механизмов, двигателей и, в частности, таких объектов, как автомобили, тепловозы, морские и речные суда, самолеты, ракеты, космические корабли и т. п. Несмотря на многообразие всех этих проблем, решения их в определенной части основываются на некоторых общих принципах и имеют общую научную базу. Объясняется это тем, что в названных задачах значительное место занимают вопросы, требующие изучения законов движения или равновесия тех или иных материальных тел.

Наука об общих законах движения и равновесия материальных тел и о возникающих при этом взаимодействиях между телами называется теоретической механикой. Теоретическая механика представляет собой одну из научных основ современных технических дисциплин.

Механикой в широком смысле этого слова называется наука, посвященная решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. В качестве материальных объектов помимо дискретных тел могут выступать среды – например, жидкость или газ и поля, поэтому круг объектов, изучаемых механикой очень широк.

В зависимости от физических свойств этих объектов и их размеров всю механику можно разделить на классическую или ньютонову и неклассическую.

Неклассическая механика - это действительно часть физики, в которой исследуются объекты микро- и макромира с учетом пространственно-временной зависимости.

Классическая механика имеет дело с объектами, протяженность которых приблизительно и с точностью до нескольких порядков заключена в интервале от 10^-10 до 10¹⁰ метра. При их изучении свойства пространства и времени можно считать постоянными. Именно такую ньютонову механику мы и будем рассматривать в дальнейшем.

В зависимости от особенностей модели реальных объектов классическая механика делится на теоретическую механику - с моделью абсолютно твердого тела и механику сплошной среды с моделью деформируемого тела.

Основным методом исследования в механике является гипотетико-дедуктивный. Его суть заключается в выдвижении гипотезы, которая подтверждается или опровергается опытом.

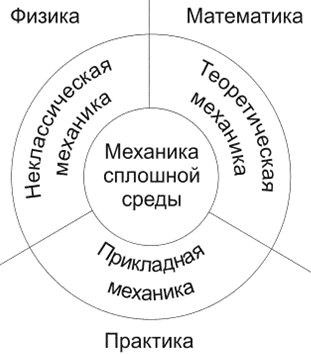
Схематически место механики в системе естествознания можно определить так, как показано на рисунке ниже. При этом механика деформируемого тела или механика сплошной среды, образующая ядро этой науки, окружена тремя сегментами, представляющими собой теоретическую механику, неклассическую механику микро- и макромира и прикладную механику, которые примыкают соответственно: к математике, физике и практике в широком смысле этого слова.

Под прикладной механикой понимают раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. Этот термин близок к понятиям «техническая» или «строительная» механика.

Теоретическая механика представляет собою часть механики, в которой изучаются общие законы движения и взаимодействия материальных тел, т.е. те законы, которые, например, справедливы и для движения Земли вокруг Солнца и для полета ракеты или артиллерийского снаряда и т. п.

Под движением в механике мы понимаем механическое движение, т.е. происходящее с течением времени изменение взаимного положения материальных тел в пространстве.

Механическим взаимодействием между телами называется тот вид взаимодействия, в результате которого происходит изменение движения этих тел или изменение их формы (деформация). Величина, являющаяся количественной мерой механического взаимодействия тел, называется в механике силой.

Основной задачей теоретической механики является изучение общих законов движения и равновесия материальных тел под действием приложенных к ним сил.

По характеру рассматриваемых задач теоретическую механику принято разделять на статику, кинематику и динамику.

Статика рассматривает частный случай механического движения, когда оно не зависит от времени – речь идет о рассмотрении равновесия твердого тела, загруженного системой сил и находящегося в состоянии покоя.

Кинематика рассматривает внешнюю сторону механического движения независимо от причин, вызвавших его. Это не что иное, как геометрия в четырехмерном пространстве, где время играет роль четвертого измерения.

Если известно положение движущейся точки в каждый момент времени, то кинематика позволяет построить ее траекторию и определить такие кинематические параметры, как скорость или ускорение.

Динамика исследует общий случай механического движения твердого тела с учетом причин, вызвавших его.

Термин «механика» впервые появляется в сочинениях одного из выдающихся философов древности Аристотеля (384—322 до н. э.) и происходит от греческого слова μηχαυή, означающего по современным понятиям «сооружение», «машина», «изобретение»

В древние времена, когда запросы производства сводились главным образом к удовлетворению нужд строительной техники, начинает развиваться учение о так называемых простейших машинах (блок, ворот, рычаг, наклонная плоскость) и общее учение о равновесии тел (статика). Обоснование начал статики содержится уже в сочинения одного из великих ученых Архимеда (287 – 212 г. но н. э.).

В России на развитие первых исследований по механике большое влияние оказали труды гениального ученого и мыслителя М. В. Ломоносова (1711—1765). Из многочисленных отечественных ученых, внесших значительный вклад в развитие различных областей теоретической механики, прежде всего, должны быть названы: М. В. Остроградский (1801—1861), которому принадлежит ряд важных исследований по аналитическим методам решения задач механики; П. Л. Чебышев (1821—1894), создавший новое направление в исследовании движения механизмов; С. В. Ковалевская (1850—1891), решившая одну из труднейших задач динамики твердого тела; И. В. Мещерский (1859—1935), заложивший основы механики тел переменной массы; К. Э. Циолковский (1857—1935), сделавший ряд фундаментальных открытий в теории реактивного движения; А. Н. Крылов (1863—1945), разработавший теорию корабля и много внесший в развитие теории гироскопических приборов.

Выдающееся значение для развития механики имели труды «отца русской авиации» Н. Е. Жуковского (1847—1921) и его ближайшего ученика С. А. Чаплыгина (1869—1942). Характерной чертой в творчестве Н. Е. Жуковского было приложение методов механики к решению актуальных технических задач. Большое влияние идеи Н. Е. Жуковского оказали и на преподавание теоретической механики в высших технических учебных заведениях нашей страны.

Стоящая в наши дни перед отечественной наукой и техникой задача непрерывного роста и внедрения в производство новой техники требует дальнейшего повышения качества подготовки инженерных кадров, расширения теоретической базы их знаний. Известную роль в решении этой задачи должно сыграть и изучение одной из научных основ современной техники – теоретической механики.

Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Для определенности рассматриваем прямоугольную декартову систему координат.

Вектор - это направленный отрезок, который характеризуется длиной и направлением.

Операции над векторами. Вектора можно складывать и умножать на число.

- сумма двух векторов есть вектор

α∙ - произведение вектора на действительное число есть вектор

- существует нулевой вектор

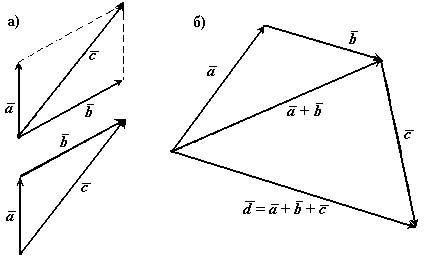
Рис.1

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам (см. рис.2):

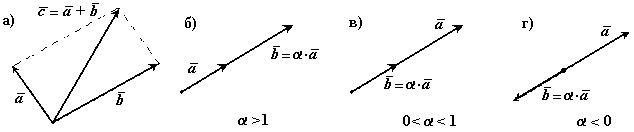
Рис.2

2. Правые и левые системы координат.

Декартовы системы координат делятся на два вида: правую и левую.

Рассмотрим декартовы системы координат на плоскости (см. рис. 3).

При повороте оси Ox правой системы координат на 90^о против часовой стрелки она совпадает с осью Oy .

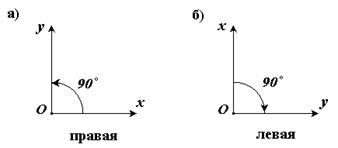
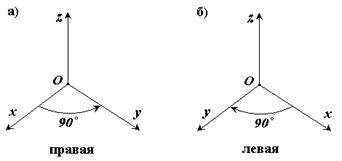
Рис.3 Рис.4

Рассмотрим декартовы системы координат в пространстве (см. рис.4).

При повороте оси Ox правой системы координат вокруг оси Oz на 90⁰ против часовой стрелки она совпадает с осью Oy .

3. Длина, проекции и направляющие косинусы вектора.

В дальнейшем будем рассматривать правую декартову систему координат. Единичные вектора вдоль осей Ox, Oy и Oz образуют систему единичных (или базисных) векторов. Любой вектор, имеющий начало в точке O, можно представить как сумму , числа (a_x, a_y, a_z) - это проекции вектора на оси координат (см. рис.5).

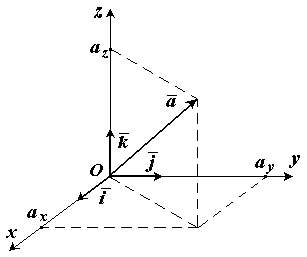
Рис.5

Длина (или модуль) вектора определяется формулой и обозначается a или ||.

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.6).

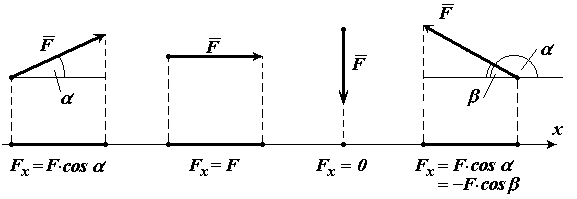
Рис.6

Направляющими косинусами вектора называются косинусы углов между вектором и положительными направлениями осей Ox, Oy и Oz соответственно.

Любая точка пространства с координатами (x, y, z) может быть задана своим радиус-вектором

Координаты (x, y, z) это проекции вектора на оси координат.

4. Скалярное произведение двух векторов

Имеется два вектора и .

,

.

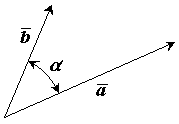
Рис.7

Результатом скалярного произведения двух векторов и является скалярная величина (число).

Записывается как или (, ). Скалярное произведение двух векторов равно

Свойства скалярного произведения:

5. Векторное произведение двух векторов

Имеется два вектора .

.

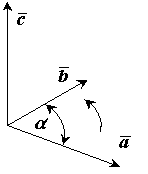
Рис.8

Результатом векторного произведения двух векторов является вектор . Записывается как или [.].

Векторное произведение двух векторов это вектор, перпендикулярный к обоим этим векторам, и направленный так, чтобы с его конца поворот вектора к вектору был виден против часовой стрелки.

Длина (или модуль) векторного произведения равна |.

Свойства векторного произведения:

Векторное произведение двух векторов вычисляется через их проекции следующим образом:

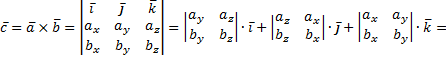
Основные понятия статики

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление материалов, теория упругости, гидродинамика и т.д.).

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

Основные понятия:

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН).

Сила является величиной векторной.

Ее действие на тело определяется: 1) численной величиной или модулем силы, 2) направлением силы, 3) точкой приложения силы (рис.9).

Например, будем прикладывать к стулу одну и ту же по модулю силу F. При приложении силы сверху вниз стул остается в состоянии покоя; при положении силы снизу вверх - стул поднимается; изменим направление нагружения, приложим силу горизонтально к спинке стула - стул опрокинется. Так как во всех случаях направление и место приложения силы различны, то и результат действия силы на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков.

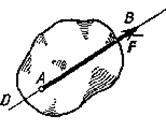
Рис.9

Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.

Прямая DE, вдоль которой направлена сила, называется линией действия силы.

Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

В тексте вектор силы обозначается латинскими буквами и др., с черточками над ними. Если черточки нет, значит у силы известна только ее численная величина - модуль.

Рис. 1.2.

Предполагается, что действие силы на тело не изменится, если ее перенести по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Например, если системы сил, изображенных на рис. 9.1, а и рис. 9.1, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.

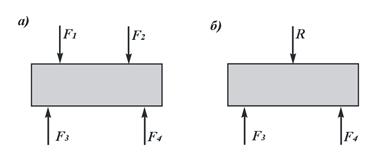
Рис.9.1. Система сил:

а – заданная система сил; б – эквивалентная система сил

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.

6. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Таким образом, равнодействующая - это сила, которая одна заменяет действие данной системы сил на твердое тело. Так как система сил F₁ и F₂ эквивалентна одной силе R (рис. 9.1, б), то сила R называется равнодействующей данной системы сил. Силы F₁ и F₂ в свою очередь могут называться составляющими силы R.

7. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, представляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равнодействующую сил тяжести его частиц. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела.

Аксиомы статики.

Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 10).

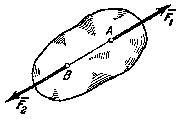
Рис.10

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.

Аксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.

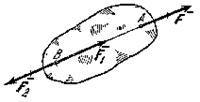
Рис.11

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.11). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы и , такие, что , . От этого действие силы на тело не изменится. Но силы и согласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В результате на тело. Будет действовать только одна сила , равная , но приложенная в точке В.

Таким образом, вектор, изображающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.

Вектор , равный диагонали параллелограмма, построенного на векторах и (рис.12), называется геометрической суммой векторов и : .

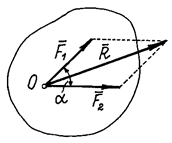
Рис.12

Величина равнодействующей

Рис. 1.3.

.

Конечно, Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.

Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой (рис. 13). Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

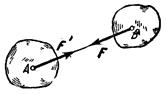
Рис.13

Этот принцип утверждает, что в природе не существует односторонних явлений. На рис. 13.1 изображена балка, опирающаяся на стены концами А и В. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами D_A и D_B, приложенными к стенам, а силы противодействия - силами R_A и R_B, приложенными к балке, которые в дальнейшем будем называть реакциями.

.

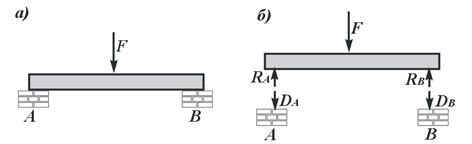
Рис. 13.1. Опирание балки на опоры:

а – схема загружения балки; б – силы действия балки на

опоры и противодействия со стороны опор на балку

Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Связи и их реакции.

По определению, тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так.

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равновесии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Одна из главных задач статики твердого тела - нахождение реакции связей. Для определения реакции связей необходимо найти величину этой реакции, линию и направление ее действия. Линия действия реакции обычно проходит через точку касания тела и связи. Численное значение реакции определяется расчетом, а направление реакции зависит от вида (конструкции) связи.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей.

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.14,а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 14,б), то реакция направлена по нормали к другой поверхности.

Если поверхности не гладкие, надо добавить еще одну силу – силу трения , которая направлена перпендикулярно нормальной реакции в сторону, противоположную возможному скольжению тела.

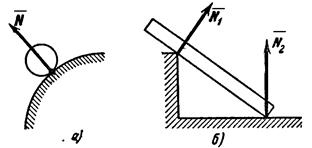
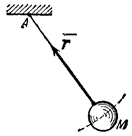
Рис.14 Рис.15

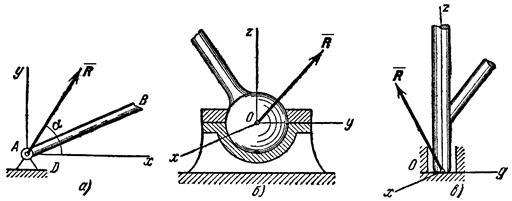
Рис.16

2. Нить (гибкие связи). Связь, осуществленная в виде гибкой нерастяжимой нити (рис.15), не дает телу М удаляться от точки подвеса нити по направлению AM. Поэтому реакция Т натянутой нити направлена вдоль нити от тела к точке ее подвеса. Если даже заранее можно догадаться, что реакция направлена к телу, все равно ее надо направить от тела. Таково правило. Оно избавляет от лишних и ненужных предположений и, как убедимся далее, помогает установить сжат стержень или растянут.

3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром; осевая линия болта называется осью шарнира. Тело АВ, прикрепленное шарниром к опоре D (рис.16,а), может поворачиваться как угодно вокруг оси шарнира (в плоскости чертежа); при этом конец А тела не может переместиться ни по какому направлению, перпендикулярному к оси шарнира. Поэтому реакция R цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной к оси шарнира, т.е. в плоскости А_ху. Для силы R в этом случае наперед не известны ни ее модуль R, ни направление (угол ).

4. Шаровой шарнир и подпятник. Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. Примерами таких связей служат шаровая пята, с помощью которой прикрепляется фотоаппарат к штативу (рис.16,б) и подшипник с упором (подпятник) (рис. 16,в). Реакция R шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее наперед неизвестны ни модуль реакции R, ни углы, образуемые ею с осями х, у, z.

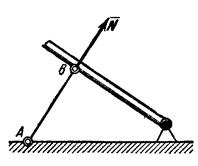
Рис.17

5. Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами (рис.17). Примем, что весом стержня по сравнению с воспринимаемой им нагрузкой можно пренебречь. Тогда на стержень будут действовать только две силы приложенные в шарнирах А и В. Но если стержень АВ находится в равновесии, то по аксиоме 1 приложенные в точках А и В силы должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня. Следовательно, нагруженный на концах стержень, весом которого по сравнению с этими нагрузками можно пренебречь, работает только на растяжение или на сжатие. Если такой стержень является связью, то реакция стержня будет направлена вдоль оси стержня.

6. Подвижная шарнирная опора (рис.17.1). Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира. Реакция такой опоры направлена по нормали к поверхности, на которую опираются катки подвижной опоры. На схемах эту связь изображают так, как показано на рис. 17.1.

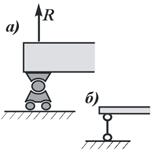
Рис.17.1. Шарнирно подвижная опора:

а – вид катковой опоры; б – расчетная схема шарнирно-подвижных опор

7. Неподвижная шарнирная опора (рис.18). Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие R_x и R_y, соответствующие направлению выбранных осей (рис. 18, а). В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис.18, б) или шарнира (рис 18, в). При решении задач будем реакцию изображать ее составляющими и по направлениям осей координат. Если мы, решив задачу, найдем и , то тем самым будет определена и реакция ; по модулю R.

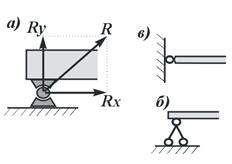
Рис.18. Шарнирно-неподвижная опора:

а – вид шарнирно-неподвижной опоры;

б, в – расчетные схемы шарнирно-неподвижных опор

Способ закрепления, показанный на рис.18, употребляется для того, чтобы в балке не возникало дополнительных напряжений при изменении ее длины от изменения температуры или от изгиба.

8. Неподвижная защемляющая опора или жесткая заделка (рис.19, а). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рис.19, а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция R_y, перемещению в горизонтальном направлении препятствует реакция R_x и повороту вокруг точки А - опорный момент М_А. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в теоретической механике показано на рис. 1.9, б. Если под такую балку где-нибудь в точке В подвести еще одну опору, то балка станет статически неопределимой.

С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.

Рис. 19. Жесткая заделка:

а – вид жесткой заделки; б – расчетная схема жесткой заделки

При определении реакций связи других конструкций надо установить, разрешает ли она двигаться вдоль трех взаимно перпендикулярных осей и вращаться вокруг этих осей. Если препятствует какому-либо движению – показать соответствующую силу, если препятствует вращению – пару с соответствующим моментом.

Иногда приходится исследовать равновесие нетвердых тел. При этом будем пользоваться предположением, что если это нетвердое тело находится в равновесии под действием сил, то его можно рассматривать как твердое тело, используя все правила и методы статики.

Связи, как и другие понятия, встречающиеся в аксиомах, являются абстракциями, весьма условно отражающими свойства реальных объектов. Например, рассмотренная выше гибкая невесомая нить может быть моделью подвесных и вантовых систем, у которых масса погонного метра троса составляет десятки и сотни килограммов. Однако усилия, возникающие в таких тросах, во столько раз больше их собственного веса, что при расчете последним можно пренебречь, считая их невесомыми.

Пример 1. На невесомую трехшарнирную арку действует горизонтальная сила (рис.20). Определить линию действия реакции (реакции связи в точке А).

Решение: Рассмотрим правую часть арки отдельно. В точках В и С приложим силы реакции связей . Тело под действием двух сил находится в равновесии. Согласно аксиоме о равновесии двух сил, силы равны по величине и действуют вдоль одной прямой в противоположные стороны. Таким образом, направление силы нам известно (вдоль линии ВС).

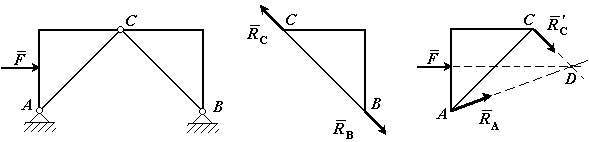
Рис.20

Рассмотрим левую часть арки отдельно. В точках А и С приложим силы реакции связей . Сила , действие равно противодействию. На тело действуют три силы, направления двух сил (и .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила направлена вдоль линии AD.

Пример 2. Однородный стержень закреплен шарнирно в точке А и опирается на гладкий цилиндр. Определить линию действия реакции (реакции связи в точке А).

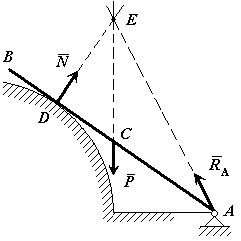
Рис.21

Решение: Так как стержень однородный, то равнодействующая сил тяжести (сила ), действующих на стержень, приложена в его геометрическом центре (точка С). Так как стержень опирается на гладкую поверхность, то реакция связи (сила ) в точке касания (точка D) направлена по нормали к этой поверхности. На тело действуют три силы, направления двух сил ( и .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила направлена вдоль линии AЕ.

Пример 3. Найти реакции связей изогнутой балки АВС, находящейся под действием плоской системы сил (рис.21). Вычисление реакций выполнить при a=1,2 м, b = 2,4 м, l = 1,8 м, α=30°, P₁ = 8 кН, P₂ = 6 кН, М=8 кНм.

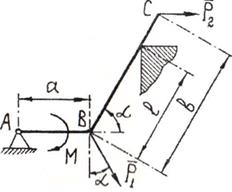
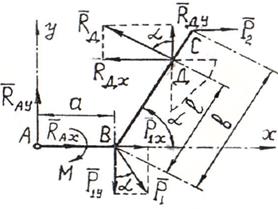
Рис.22 Рис.23

Решение. Освободим балку от связей и приложим к ней реакции связей. На рис.22 - составляющие реакции шарнира А вдоль осей координат - реакция выступа стены ( перпендикулярно ВС).

Разложим силы и на составляющие вдоль осей координат

Условия равновесия балки имеют вид

После решения составленной системы уравнений получаем

Вопросы для самопроверки

- В чем состоит предмет статики?

- Что такое материальная точка? Система материальных точек?

- Что такое абсолютно твердое тело?

- Какие величины называются векторными и скалярными?

- Что называется моментом силы относительно данной точки и какова его размерность?

- Что называется реакциями связей?

- Что такое статически эквивалентная система сил?

- Что такое аксиомы статики твердого тела? Как они формулируются?

- Приведите определение понятия «сила».

- Какими приборами измеряют численное значение силы?

- Какими единицами измеряется сила в Международной системе (СИ)?

- Перечислите признаки, характеризующие силу.

- Что называется системой сил?

- Приведите примеры сосредоточенных и распределенных сил.

- Что называется равнодействующей системы сил?

- Какая сила называется уравновешивающей?

- Дайте определение внешней и внутренней силы.

- Сформулируйте аксиому о равновесии двух сил.

- Какие системы сил называются эквивалентными?

- Что такое равнодействующая и уравновешивающая сила?

- Какие системы сил называются статически эквивалентными?

- В чем сходство между равнодействующей и уравновешивающей сил и чем они друг от друга отличаются?

- Сформулируйте первую, вторую, третью и четвертую аксиомы статики.

- К двум различным точкам твердого тела (см. рис.) приложены две непараллельные, но действующие в одной плоскости силы. Можно ли для сложения этих сил применить правило параллелограмма?

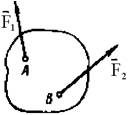
- Можно ли силу в 50 Н разложить на две силы, например, по 200 Н?

- Сформулируйте пятую аксиому статики.

- Что называют связью?

- Какие разновидности связей рассматриваются в статике?

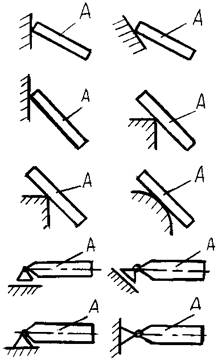
- Изменится ли направление реакций связей, если, не меняя положение бруса А, изображенные на рис. а опоры (связи) заменить опорами (связями), как показано на рис. б? (Трение не учитывать, т. е. связи считать идеальными).

- Назовите простейшую систему сил, эквивалентную нулю.

- В чем заключается сущность аксиомы присоединения и исключения уравновешивающихся сил?

- Назовите сущность аксиомы отвердевания.

- Сформулируйте правило параллелограмма сил.

- Что выражает аксиома инерции?

- Приведите формулировку аксиомы равенства действия и противодействия.

- Что называется связью, наложенной на твердое тело?

- Что такое реакция связи?

- Что называется силой реакции связи?

- Сформулируйте принцип освобождаемости от связей.

- К какому объекту приложены силы реакций?

- Перечислите основные виды связей, для которых заранее известно направление силы реакции.

- Назовите связи, для которых заранее известна точка приложения реакции, но не ее направление.

- В чем сущность принципа освобождаемости от связей?

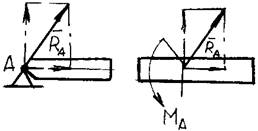
- Как направлена реакция опорного шарнира, если твердое тело соединено с опорой с помощью стержня, имеющего на концах шарниры?

- Почему со стороны неподвижного шарнира на брус действует только сила R_A (реакция шарнира), а при жесткой заделке бруса на него действуют и сила R_A, и реактивный момент M_A заделки (см. рис.)?

- Абсолютно твердым телом называется, такое тело

1) расстояние между каждыми двумя точками которого остаются всегда неизменными;

2) размеры каждого очень мало по сравнению другими телами;

3) форма тело остается постоянной;

4) в котором можно пренебречь формой;

5) которое деформируется.

- Статикой называется раздел теоретической механики:

1) в которой изучаются условия равновесия материальных тел под действием сил;

2) в которой изучается силы реакции связи;

3) в которой рассматривается движения тела, относительно подвижного отчета;

4) в которой изучаются связи;

5) в которой изучаются общие законы движения.

- Сила определяется:

1) модулем, направлением, точкой приложения;

2) весом;

3) направлением;

4) величиной;

5) равнодействующей.

- Что называется силой?

1) мера взаимодействие тел;

2) перемещение тел;

3) мера веса;

4) мера тяготения;

5) механическое воздействие.

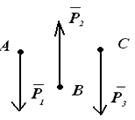
- На рисунке изображена …

1) пересекающая система сил;

2) параллельная система сил;

3) система плоских сил;

4) силы реакции связи;

5) произвольная система сил.

- На рисунке изображена:

1) параллельная система сил;

2) пересекающая система сил;

3) система плоских сил;

4) силы реакции связи;

5) произвольная система сил.

- Почему действующая сила и сила противодействия не уравновешиваются?

1) действует на разное тело;

2) они направлены противоположные стороны;

3) модуль сил не равны между собой;

4) они направлены по одной прямой;

5) направлены в одну сторону.

- Силы бывает в зависимости от времени:

1) динамической;

2) распределенной;

3) сосредоточенной;

4) объемной;

5) уравновешенной.

- Силы бывает в зависимости от времени:

1) статической;

2) распределенной;

3) сосредоточенной;

4) объемной;

5) уравновешенной.

- Система сил, линия действия которых пересекается в одной точке называется:

1) системой сходящихся сил;

2) системой пересекающихся сил;

3) системой параллельных сил;

4) парой сил;

5) произвольно расположенной силой.

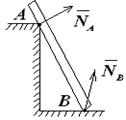
- Какой вид связи изображен на рисунке?

1) гладкая поверхность;

2) плоскость;

3) подвижный шарнир;

4) жесткое защемление;

5) поверхность.

- Когда деформация тела не учитывается?

1) при расчете равновесия;

2) при расчете прочности;

3) при расчете жесткости;

4) при расчете устойчивости;

5) при определении движения.

- Основная задача статики:

1) определить условия равновесия сил;

2) определить силу;

3) определить сил реакции опор;

4) найти равнодействующую силу;

5) определить абсолютно твердое тело.

- При каком значении угла между линиями действия двух сил их равнодействующая определяется по формуле:

1)

2) ;

3) .

- В каких связях перечисленных ниже, реакции всегда направлены по нормали к поверхности?

1) гладкая плоскость;

2) гибкая связь;

3) жесткий стержень;

4) шероховатая поверхность.

- К чему приложена реакция опоры?

1) к самой опоре;

2) к опирающемуся телу.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00