Главная

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

17.1. Кривошип ОА, вращаясь с угловой скоростью и угловым ускорением вокруг оси О неподвижной шестеренки 1 радиусом R₁, приводит в движение насаженную на его конце А шестеренку 2 радиусом R₂.

Определить ускорения точек В и С подвижной шестеренки.

Дано: , , , , .

Найти: , .

Решение: Скорость точки А колеса и ее ускорение соответственно будут:

и

.

Возьмем за полюс центр колеса (точку А). Мгновенный центр скоростей в точке соприкосновения шестеренок 1 и 2 (точка Р). Угловая скорость 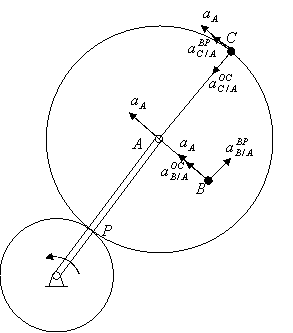колеса:

.

Качение шестеренки 2 без проскальзывания, поэтому угловое ускорение шестеренки 2:

.

Зная и , определим модули осестремительного и вращательного ускорений точки В и С вокруг полюса А:

и

и .

Ускорение точек:

и

.

В скалярном виде:

,

.

17.2. Кривошип ОА, вращаясь с угловой скоростью и угловым и ускорением вокруг оси О неподвижной шестеренки 1 радиусом , приводит в движение насаженную на его конце А шестеренку 2 радиусом .

Определить ускорения точек В и С подвижной шестеренки.

Дано: , , , .

Найти: , .

Решение: Скорость точки А колеса и ее ускорение соответственно будут:

и

.

Возьмем за полюс центр колеса (точку А). Мгновенный центр скоростей в точке соприкосновения шестеренок 1 и 2 (точка Р). Угловая скорость колеса:

.

Качение шестеренки 2 без проскальзывания, поэтому угловое ускорение шестеренки 2:

.

Зная и , определим модули осестремительного и вращательного ускорений точки В и С вокруг полюса А:

и

и .

Ускорение точек:

и

.

В скалярном виде:

.

20.1. Проволочная окружность радиусом вращается в своей плоскости вокруг точки О с угловой скоростью . На окружность надето колечко М, которое может скользить по неподвижному стержню АВ.

Найти абсолютную скорость колечка М и его скорость относительно окружности в заданном положении.

Дано: , , .

Найти: , .

Решение:

1)Сделаем расчетную схему с указанием колечка М в заданном положении. И покажем скорости относительного движения , переносного движения и абсолютного движения .

2) Из рисунка видно, что , поэтому относительная скорость точки М:

.

Так как угол между и равен 45⁰:

,

Откуда:

.

20.2. Проволочная окружность радиусом вращается в своей плоскости вокруг точки О с угловой скоростью . На окружность надето колечко М, которое может скользить по неподвижному стержню АВ.

Найти абсолютную скорость колечка М и его скорость относительно окружности в заданном положении.

Дано: , , .

Найти: , .

Решение:

1)Сделаем расчетную схему с указанием колечка М в заданном положении.

2) Из рисунка видно, что , поэтому относительная скорость точки М:

.

Так как ,

Откуда:

.

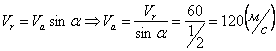20.3. Проволочная окружность радиусом вращается в своей плоскости вокруг точки О с угловой скоростью . На окружность надето колечко М, которое может скользить по неподвижному стержню АВ.

Найти абсолютную скорость колечка М и его скорость относительно окружности в заданном положении.

Дано: , , .

Найти: , .

Решение:

1)Сделаем расчетную схему с указанием колечка М в заданном положении.

2) Из рисунка видно, что и , поэтому относительная скорость точки М:

.

3) Видно, что

20.4. Стержень ОА вращается вокруг точки О с угловой скоростью . На стержень надето колечко М, которое может скользить по неподвижной проволочной окружности радиусом .

Найти абсолютную скорость колечка М и его скорость относительно стержня в момент, определяемый углом .

Дано: , , .

Найти: , .

Решение:

1)Расчетная схема нарисована в соответствии с исходными данными.

2) Анализ движения кольца М:

- Относительное движение кольца М по стержню ОА.

- Переносное движение – вращение стержня ОА, вокруг оси О.

- Абсолютное движение – движение кольца М по окружности радиуса .

3) Проводим через точку М линии скоростей:

- Линия r-r проведена вдоль ОА – траектории относительного движения;

- Линия e-e проведена перпендикулярно ОА – так направлена скорость точки М стержня ОА (переносная скорость )

- Так как траектория абсолютного движения кольца М – окружность с центром в точке С, поэтому линия а-а проведена по касательной к этой окружности.

Из рисунка видно, что:

.

И тогда:

.

Из схемы на рисунке видно, что:

.

Откуда абсолютная скорость кольца М:

.

20.5. Окружность радиусом 30см перемещается в своей плоскости поступательно со скоростью , передвигая колечки М₁ и М₂ по неподвижному стержню АВ.

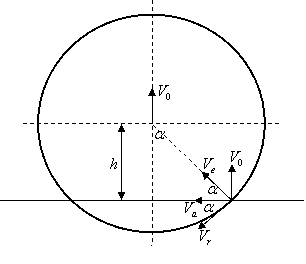Дано: , , .

Найти: , .

Решение: Из расчетной схемы видно, что:

и

.

Абсолютная скорость точки М:

,

Относительная скорость точки:

.

23.1. В вагоне, движущимся по прямолинейному участку пути рельсу с ускорением а, подвешен стержень ОА, который совершает колебательное движение по закону в вертикальной плоскости вокруг оси О, перпендикулярной к направлению движения вагона.

Определить для указанного момента времени t абсолютное ускорение точки А стержня.

Дано: , , , .

Найти: .

Решение: Угол в заданный момент времени:

.

Угловая скорость стержня:

.

Угловое ускорение стержня:

.

Нормальное ускорение точки А:

Касательное ускорение точки А:

.

Общее ускорение точки А складывается по формуле:

.

В скалярном виде, как видно из рисунка:

.

23.2. Тележка движется по прямолинейному участку пути с ускорением . На продольном валу тележки находится маховичок радиусом , который вращается согласно уравнению .

Определить абсолютное ускорение точки обода маховика для заданного момента времени .

Дано: , , , .

Найти: .

Решение:

Угловая скорость стержня:

.

Угловое ускорение стержня:

.

Нормальное ускорение точки А:

Касательное ускорение точки А:

.

Общее ускорение точки А складывается по формуле:

.

В скалярном виде, как видно из рисунка:

.

23.3. Тележка движется по прямолинейному участку пути с ускорением . На продольном валу тележки находится маховичок радиусом , который вращается согласно уравнению .

Определить абсолютное ускорение точка обода маховика для заданного момента времени .

Дано: , , , .

Найти: .

Решение: Угловая скорость диска в заданный момент:

,

Угловое ускорение диска в заданный момент:

.

Осестремительное и тангенциальное ускорения точки обода колеса соответственно:

и

.

Абсолютное ускорение точки колеса:

,

А в скалярном виде:

.

23.4. К валу электрического двигателя, согласно уравнению , прикреплен под прямым углом стержень ОА длиной . 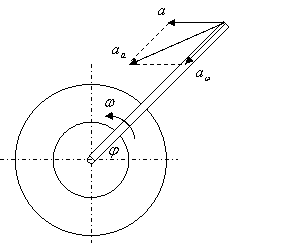Двигатель совершает горизонтальные колебания на фундаменте по закону .

Определить для заданного момента времени абсолютное ускорение точки А стержня.

Дано: , , , , .

Найти: .

Решение: Вычертим расчетную схему с заданными параметрами и покажем ускорения.

Осестремительное ускорение стержня в точке А:

.

Горизонтальное ускорение системы:

.

Абсолютное ускорение точки А:

.

25.1. Стержень ОА вращается вокруг точки О с угловой скоростью . Вдоль стержня движется точка М, положение которой определяется заданным расстоянием .

Найти абсолютное ускорение точки М в момент времени .

Дано: , .

Найти: .

Решение: Расстояние S точки М в заданный момент времени:

.

Ускорение точки М по стержню АО:

.

Угловая скорость стержня АО:

.

Осестремительное ускорение точки М:

.

Угловое ускорение стержня АО:

.

Касательное ускорение точки М:

.

Общее ускорение точки М:

.

В скалярном виде будет:

.

25.2. Квадрат OABC, сторона которого равна 24см, вращается в своей плоскости с постоянной угловой скоростью вокруг вершины О. В некоторый момент времени из вершины В по стороне ВС начинает двигаться точка М по закону .

Дано: , , .

Найти: .

Решение: Величина в заданный момент времени будет:

.

Ускорение этой точки по стороне ВС:

.

Из рисунка видно, что:

и

.

Ускорение точки М относительно вращения вокруг точки О:

.

Абсолютное ускорение точки М:

,

В векторном виде будет:

.

25.3. Диск радиусом вращается с постоянной угловой скоростью вокруг оси С, перпендикулярной к плоскости диска. По хорде АВ относительно ее середины О колеблется точка М по закону .

Найти абсолютное ускорение точки М в данный момент времени .

Дано: , , , .

Найти: .

Решение: Найдем величину х в заданный момент времени:

,

Ускорение точки М по хорде АВ:

.

Из рисунка видно, что:

,

.

Осестремительное ускорение точки М:

.

Абсолютное ускорение точки М:

.

25.4. Диск радиусом вращается с угловой скоростью вокруг оси С, перпендикулярной плоскости диска. По диаметру АВ относительно центра О диска колеблется точка М по закону .

Найти абсолютное ускорение точки М в заданный момент времени.

Дано: , , , , .

Найти: .

Решение: Смещение точки х к заданному моменту времени:

.

Ускорение точки по диаметру АВ:

.

ускорение точки М вокруг точки С:

.

Абсолютное ускорение точки М:

.

25.5. Точка M движется относительно тела D. По заданным уравнениям относительного движения точки M и движения тела D определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки M.

Дано: Cхема механизма (рис. 1), , , , , .

Найти: абсолютные скорость и ускорение точки М.

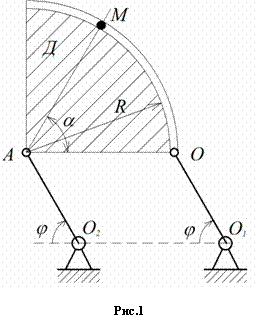Решение. Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью Д. Положение точки M на теле Д определяется расстоянием .

При ,

Угол вычисляется из длины дуги ОМ

,

откуда находим значение угла

.

Абсолютную скорость точки M найдем как геометрическую сумму относительной и переносной скоростей:

.

Модуль относительной скорости

,

где .

При t = 2 с

, .

Положительный знак у показывает, что вектор направлен в сторону возрастания .

Модуль переносной скорости

, (1)

где точка M, как и AO участвует в поступательном движении тела Д (т.е. AO всегда параллельна самой себе).

.

При t = 2 c

.

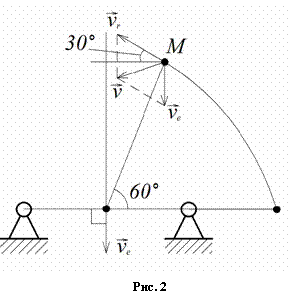Направление совпадает с направлением отсчета угла , следовательно, вектор направлен перпендикулярно плоскости чертежа от нас.

Тогда, согласно формуле (1) модуль переносной скорости:

.

Вектор направлен по касательной к окружности O₂A в сторону вращения тела Д. В момент времени t = 2 c положение тела Д таково, что значение угла составляет рад. Следовательно, вектор направлен вертикально вниз (рис. 2.8). Так как вектор не перпендикулярен вектору , то для нахождения модуля абсолютной скорости используем теорему косинусов:

Абсолютное ускорение точки M равно геометрической сумме относительного, переносного и кориолисова ускорений:

или в развернутом виде

Модуль относительного касательного ускорения

,

.

При t = 2 c

.

Знаки и одинаковы, следовательно, относительное движение точки М ускоренное.

Относительное нормальное ускорение

.

Угловое переносное ускорение находим как

.

При t = 2 c

Модуль переносного центростремительного ускорения

,

а модуль переносного вращательного ускорения

.

При t = 2 c

, .

Модуль кориолисова ускорения

.

Так как вектор направлен перпендикулярно плоскости чертежа от нас, то угол между направлениями векторов и равен , и тогда .

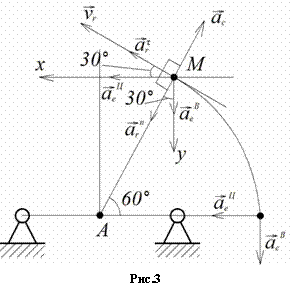
Покажем направление ускорений точки M в момент времени (рис.3). Вектор направлен по правилу векторного произведения вдоль направления MА.

Модуль абсолютного ускорения точки М находим способом проекций:

,

,

.

После вычисления получаем:

25.6. Круглая пластина R = 60 см вращается вокруг неподвижной оси по закону . По дуге окружности R движется точка по закону .

Дано: R=60 см; ; l=R; ; t₁= 1 c.

Определить: V_абс и a_абс.

Указания. Задача – на сложное движение точки. Для ее решения следует воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, необходимо по условиям задачи определить, где находится точка М на пластине в момент времени t₁ =1 с, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче).

Решение. Рассмотрим движение точки М как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

,

,

где ,

.

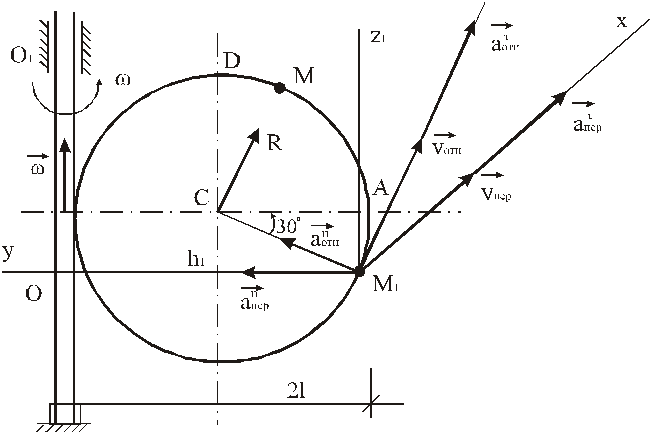
Определим все входящие в равенство величины.

1. Относительное движение

Это движение происходит по закону

.

Установим, где будет находиться точка М на дуге окружности в момент времени t₁, полагая, что t₁ = 1 c:

.

Знак «минус» свидетельствует о том, что точка М в момент времени t₁=1 c находится снизу от точки А. Изображаем ее в этом положении:.

Находим числовые значения , :

м/с.

м/с².

м/с².

Вектор направлен к центру C окружности, векторы и направлены в сторону положительного отсчета.

2. Переносное движение

Это движение происходит по закону .

Найдем сначала угловую скорость и угловое ускорение переносного вращения:

, ,

при t₁ = 1 c, c^-1, c^-2.

Для определения находим сначала расстояние h₁ =О^/М₁ точки М₁ от оси вращения.

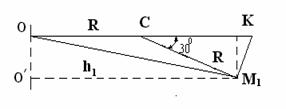
СК =Rcos30⁰ =0,52 м,

ОК =СК + R =1,12 м,

М₁О^/ = ОК=1,12 м.

Находим: =224 см/с, =448 см/с²,

=448 см/с².

Изобразим векторы и перпендикулярно плоскости DAO^/, а вектор – по линии МO^/ к оси вращения.

3. Кориолисово ускорение

Т.к. угол между вектором и осью вращения (вектором ) равен 30⁰, то численно в момент времени t₁ =1 с

=2·0,31·2·(1/2) =0,68 см/с².

Направление найдем по правилу Жуковского. Для этого вектор спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору ), и затем эту проекцию повернем на 90⁰ в сторону , т.е. против хода часовой стрелки. Получим направление вектора . Он направлен перпендикулярно плоскости пластины так же, как и вектор .

4. Определение V_абс и а_абс Т.к. , а векторы и взаимноперпендикулярны, то

= 234 см/с.

По теореме о сложении ускорений

.

Для определения а_абс проведем координаты М₁хуz и вычислим проекции а_абс на эти оси. Векторы и лежат на оси х, а векторы и расположены в плоскости М₁уz₁, т.е. в плоскости пластины.

Проецируя обе части равенства на оси М₁хуz, получаем:

а_{абс х} = =448,62 см/с²,

а_{абс z} = · =1,71 см/с²,

а_{абс у} = =449,08 см/с².

Находим затем а_абс. а_абс = =634,8 см/с².

Ответ: V_абс =234 см/с; a_абс =634,8 см/с².

25.7. Рейка 4 находится в зацеплении со ступенчатым колесом 3, связанным ременной передачей с колесом 2, которое находится в зацеплении с колесом 1, на которое намотана нить с грузом 5 (рис). Закон изменения угловой скорости колеса 1 – .

Дано: R₁ =4 см, r₁= 2 см, R₂ =8 см, r₂ =6 см, r₃ =12 см, R₃ = 16 см, , t₁=1 с.

Определить: V₅, V_B, , a_C, a₄ в момент времени t =t₁.

Указания. Задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит.

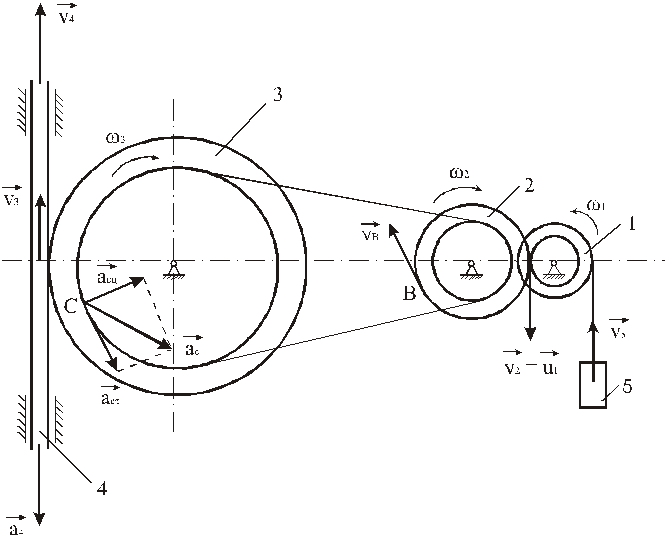
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса R_і) через V_і, а точек, лежащих на внутренних ободах (радиуса r_і), – через u_і.

1. определяем V₅. Так как V₅ = V₁, то V₅ = V₁ = = (5t – 4t²) R₁.

Для момента времени t₁=1 с

V₅ =4 см/с.

2. Определяем V_B. Так как колеса 1 и 2 находятся в зацеплении, то V₂ =u₁ и _.

.

Тогда V_B = =2(5t –4t²).

Для момента времени t₁=1 с V_B=2 см/с.

3. Определяем . По определению углового ускорения .

Для момента времени t₁=1 с ε₂ =-3/4 = -0,75 с^-2.

4. определяем a_C.

Для точки С , где численно , .

Поэтому необходимо найти и . Так как колеса 2 и 3 соединены ременной передачей, то u₂ = u₃,

,

,

.

Для момента времени t₁=1 с

=0,125 с^-1;

= -0,375 с^-2.

Тогда =0,19 см/с², =-4,5 см/с²,

=4,5 см/с².

5. Определяем а₄. Так как рейка 4 и колесо 3 находятся в зацеплении, то V₄=V₃,

.

Тогда .

Для момента времени t₁=1 с а₄ = -6 см/с².

Ответ: V₅ =4 см/с, V_B=2 см/с, = -0,75 с^-2, а_С =4,5 см/с², а₄= =-6 см/с².

25.8. Для механизма, схема которого показана на рисунке, определить скорости и ускорения точки М и тела 3, а также угловые скорости и угловые ускорения тел 1 и 2, если дано: , , , , рад, .

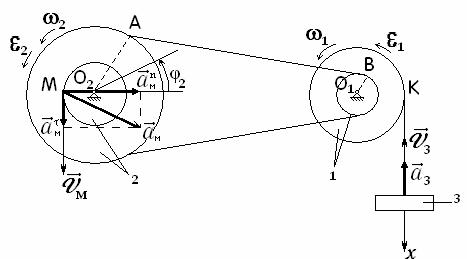
Решение. Согласно условию задачи вычерчиваем схему механизма (см. рисунок).

Используя закон движения тела 2 найдем его угловую скорость и угловое ускорение.

, ,

,

Определим скорость и ускорение точки М

, ,

, ,

, ,

.

Сравнивая линейные скорости тел 2 и 1 в точках A и B, установим соотношение ,

откуда , .

Теперь , .

Сравнивая линейные скорости в точке К, находим , .

Ускорение тела 3 будет равно , .

Направление векторов показано на рисунке.

Ответ: м/с; м/с²; м/с; м/с²; с^-1; с^-1; с^-1; с^-1;

25.9. Треугольная пластина АВО (см. рисунок) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, согласно закону рад. По стороне АВ пластины перемещается точка М по закону см. Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t₁ = 1c, если ОА = ОВ = 5 см и угол АОВ прямой.

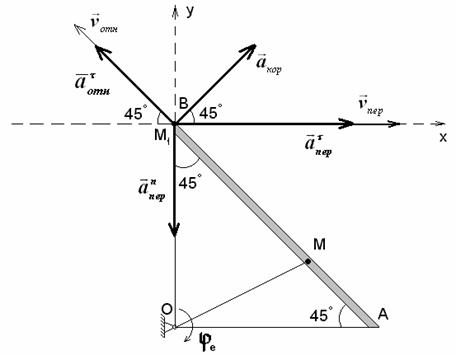
Решение. Согласно условию задачи нарисуем схему механической системы, (см. рисунок), и определим относительное положение точки см.

Положение точки М₁ показано на чертеже. Учитывая, что движение точки М сложное, при этом переносное движение (движение пластины) вращательное, а относительное движение (движение точки М по пластине) прямолинейное, то абсолютную скорость и абсолютное ускорение определим по формулам

,

где

, см/с,

, см/с²

, ,

, с^-1,

, с^-2,

, см/с,

, см/с²,

, см/с²,

,

см/с².

Направление векторов всех кинематических характеристик точки М₁ указаны на рисунке. Используя метод проекций находим:

,

,

Следовательно, модуль абсолютной скорости точки М равен

см/с,

см/с

Тогда модуль абсолютного ускорения определяется

см/с²

Ответ: см/с, см/с².

25.10. Рассмотрим пример решения задания для механизма, кинематическая схема которого приведена на рис.1, где ведущим звеном является груз.

Дано: закон изменения вертикальной координаты груза x(t) = 30 + 10t², см; радиусы колес R₁ = R₃ = 10 см, R₂ = 30 см, r₂ = 20 см.

Определить: скорость и ускорение точки М для момента времени t₁ = 1 c.

Рис.1

Решение: Обозначим и покажем на рис. 2 точки механизма А, В, D₁, D₂, через которые передается движение от одного звена (ведущего) к другому (ведомому).

Решение задачи начнем с определения скорости груза. Поскольку груз совершает поступательное движение, его можно считать точкой, движение которой задано координатным способом, и движется только вдоль оси x. Проекцию скорости груза на эту ось определим как производную от координаты x по времени , при t₁ = 1 с v_x= 20 см/с.

Поскольку знак проекции скорости груза на ось x положительный, вектор скорости направлен вниз, т.е. в положительном направлении оси x.

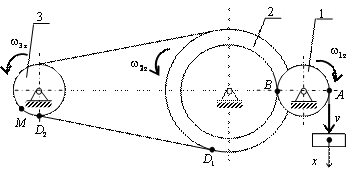
Рис.2

Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана (колеса 1) равна скорости груза. Но точка А схода нити в данный момент времени принадлежит и колесу 1, совершающему вращательное движение вокруг неподвижной оси, что позволяет определить его угловую скорость. Направление угловой скорости колеса 1 соответствует направлению скорости точки А. Запишем теперь алгебраическое значение угловой скорости колеса 1

, при t₁= 1с w_1z= 2 рад/с.

Колеса 1 и 2 находятся в зацеплении и имеют общую точку В (см. рис.2). Поэтому скорости точек колес, находящихся на их ободьях, одинаковы. При записи алгебраического значения угловой скорости колеса 2 учтем, что внешнее зацепление меняет направление вращения на противоположное

, при t₁ = 1 с w_2z = 1 рад/с.

Одинаковы также скорости точек D₁ и D₂ , расположенных на шкивах ременной передачи. Однако здесь направление вращения не изменяется, поэтому

, при t₁ = 1 с

Определим теперь скорость точки M колеса 3 в момент времени t₁ = 1 с. Величина скорости – это произведение модуля угловой скорости на расстояние от точки M до оси вращения, которое равно радиусу , Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис.3).

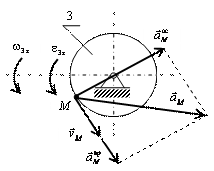
Рис.3

Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.

Ускорение точки M определим как геометрическую сумму векторов вращательного и осестремительного ускорений, модули которых вычислим по формулам:

,

откуда получим полное ускорение точки M

.

Векторы ускорений показаны на рис. 3. Движение колеса 3 ускоренное, поэтому вращательное ускорение точки M направлено в ту же сторону, что и ее скорость. Осестремительное ускорение всегда направлено к оси вращения.

Если в условии будет задан не закон движения груза x(t), а зависимость угла поворота колеса 1 от времени, например, , рад, изменения в решении задачи коснутся только начального этапа. Алгебраическое значение угловой скорости колеса 1 определим как производную от его угла поворота по времени рад/с.

Дальнейшее решение задачи не отличается от приведенного примера.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00