Главная

Тема 36. Кинематика сплошной среды

Идея Эйлера о необходимости выделения кинематики очень важна для исследования движения упругих деформируемых тел. После того как оказались бесплодными попытки создать молекулярную механику на основании взаимодействия между молекулами, выражаемого силами, законы которых оставались неизвестными, нужно было обратиться к рассмотрению перемещений, которые совершаются в непрерывной среде, не учитывая причин, вызывающих эти перемещения. Кроме того, пришлось изменить основной элемент: первоначально рассматривалась материальная точка, совершавшая только поступательные перемещения, а теперь пришлось взять бесконечно малый параллелепипед, сплошь заполненный массой и способный не только производить поступательное перемещение, но и вращаться и даже изменять свою форму. В связи с этим изменялся и характер математики: кроме обыкновенного механического движения в математику вошло и понятие о преобразовании, вызванное новыми операциями. Понятие о материальной точке, совершающей поступательные перемещения, осталось вполне пригодным для определения места бесконечно малого элемента.

Движение любой материальной системы считается известным, если для любого момента времени можно устанавливать положение любого элемента этой системы, который в рассматриваемом случае можно считать точкой. Пусть x₀, y₀, z₀ — координаты, определяющие положение некоторой точки системы в начальный момент времени t = 0; знание этих начальных координат позволяет выделить эту точку, индивидуализировать ее среди остальных.

Движение системы является вполне определенным, рели для любого момента времени t знать положение точки, координаты которой в начальный момент времени были x₀, y₀, z₀. Координаты х, у, z нового положения точки, очевидно, являются функциями времени t и начальных ее координат. Тогда

Предполагая, что система материальных точек сохраняет свою непрерывность и не распадается с течением времени, можно положить, что приведенные выше функции являются конечными и непрерывными.

Если сообщить времени t определенное значение, то разность между конечными и начальными координатами определит перемещение соответствующей точки. Это перемещение можно представить как прямолинейный отрезок, соединяющий начальное и конечное положение рассматриваемой точки; тогда функции х, у, z можно представить в таком виде:

Полученные уравнения можно рассматривать как уравнения некоторого преобразования, которому подвергаются координаты любой точки системы. Если коэффициенты а_ij являются постоянными, то эти преобразования носят названия аффинных.

Нетрудно видеть, что если решить приведенные выше уравнения относительно х_о, у_о, z_o то значения х_о, у_о, z_o выразятся через х, у, z тоже при помощи линейных уравнений, которые определят обратный переход из конечного положения в начальное; поэтому и начальные и конечные положения являются в известной степени равноправными.

Возьмем теперь в системе совокупность точек, лежащих в одной плоскости, уравнение которой имеет вид

Если вместо х, y, z подставить их значения из приведенных уравнений, то координаты х_о, у_о, z_o тоже удовлетворят уравнениям первой степени с постоянными коэффициентами; иными словами, начальные положения точек тоже будут лежать в некоторой плоскости. Это значит, что при помощи аффинных преобразований одна плоскость преобразуется тоже в плоскость.

Так как прямую линию можно определить как пересечение двух плоскостей, то в аффинных преобразованиях прямая тоже преобразуется в прямую и точка пересечения двух прямых преобразуется тоже в точку пересечения двух прямых, получившихся в результате преобразования из первых. Угол между преобразованными прямыми, однако, вообще не равен углу между первоначальными прямыми.

Две параллельные прямые можно рассматривать как пересекающиеся в бесконечно удаленной точке. Но из уравнений преобразования следует, что конечным значениям х_о, у_о, z_o всегда соответствуют тоже конечные значения х, у, z, и наоборот, для того чтобы одна или все координаты х, у, z получили бесконечные значения, необходимо, чтобы одна или несколько координат, х_о, у_о, z_o тоже имели бы бесконечно большие значения. Это показывает, что прямые, бывшие параллельными до преобразования, остаются параллельными и после этого преобразования.

Рассмотрим теперь частные случаи аффинных преобразований. Предположим сначала, что коэффициенты a₁₀, a₂₀, a₃₀ имеют любые значения, а из остальных a₁₁=a₂₂=a₃₃=1 и все а_ij при i≠j равны нулю; в таком случае уравнения преобразования примут вид

Это показывает, что приведенное преобразование соответствует поступательному перемещению, когда все точки получают одинаковые перемещения, проекции которых на координатные оси будут

Таким образом, из каждого аффинного преобразования можно выделить часть, соответствующую поступательному перемещению.

После выделения этой части уравнения аффинного преобразования примут вид:

Эти уравнения очень похожи на уравнения, дающие преобразования системы координат, когда сохраняется начало координат О:

Такое преобразование представит вращение координатной системы вокруг начала координат, если между коэффициентами а_ij будут существовать отношения, характерные для направляющих косинусов. Можно показать, что во всяком аффинном перемещении содержится перемещение, соответствующее вращению вокруг оси, проходящей через начало координат О.

Вокруг начала координат опишем сферу радиусом единицей:

и подставим вместо х, у, z их выражения:

Нетрудно видеть, что после произведения преобразований полученное уравнение можно привести к виду

Это равенство есть уравнение поверхности второго порядка, не имеющей бесконечно удаленных точек, т. е. полученная поверхность является эллипсоидом.

Но всякий эллипсоид имеет три взаимно перпендикулярных сопряженных диаметра, его главные оси. Эти главные оси получаются из трех сопряженных диаметров первоначальной сферы; таким образом, эти три взаимно перпендикулярные прямые в результате преобразования поворачиваются на некоторый угол вокруг какой-то оси, проходящей через неподвижную точку.

Если выделить и это преобразование, то остаточная часть аффинного преобразования сведется к такому преобразованию, которое переводит шар в эллипсоид, а это преобразование соответствует растягиванию или сжиманию шара по трем взаимно перпендикулярным направлениям.

Если эти направления совпадают с направлениями координатных осей, то упомянутое преобразование можно выразить при помощи уравнений

Если х_о, у_о, z_o рассматривать как стороны прямоугольного параллелепипеда, то объем параллелепипеда, полученного после преобразования, будет

Для выполнения всего преобразования требуется определить коэффициенты расширения по трем главным осям; три неизвестных потребуются для определения направлений осей, по которым производятся линейные расширения; выполнение самого вращения тоже потребует трех неизвестных, например значений трех эйлеровых углов собственного вращения, нутации и прецессии. Эти девять неизвестных величин определятся по девяти заданным коэффициентам аффинного преобразования. Для выполнения этого преобразования было введено новое математическое понятие, получившее название тензора. Слово «тензор» происходит от латинского tendo — тяну, натягиваю.

Пусть в данной системе координат Oxyz задан вектор координатами (х, у, z). B другой системе координат Ox^/y^/z^/ направляющие косинусы осей по отношению к прежним заданы следующей таблицей:

	Ox Oy Oz
Ox^/	a₁₁ a₁₂ a₁₃
Oy^/	a₂₁ a₂₂ a₂₃
Oz^/	a₃₁ a₃₂ a₃₃

Новые координаты x^/, y^/, z^/ данного вектора выразятся формулами

Считаем, отвлекаясь от геометрического смысла данного преобразования, что имеются две векторные величины и связанные указанным преобразованием. Зависимость между этими величинами можно выразить так:

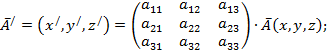
вектор рассматривается как полученный из вектора при помощи умножения на оператор, который носит название матрицы.

Векторы можно представить тоже в виде матриц:

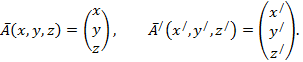
Тогда

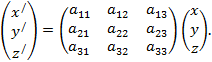
Это значит, что можно установить определенное правило умножения матриц: координаты произведения получаются как суммы последовательных произведений координат множимой матрицы на элементы, стоящие сначала в первой строке матрицы, затем во второй и, наконец, в третьей, как можно убедиться из вышеприведенных формул преобразования:

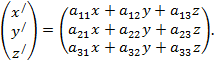
Правило умножения матриц можно распространить и на более сложные случаи.

Пусть имеется два последовательных преобразования:

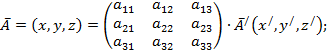
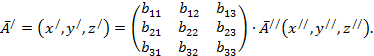
Преобразование, переводящее в , можно представить в виде произведения:

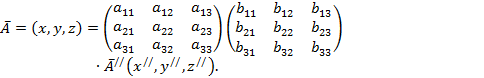
Отметим, что переместительный закон для умножения матриц неприменим: все умножения нужно производить в том же порядке, в каком стоят множители.

Положим

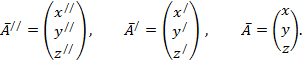
Тогда

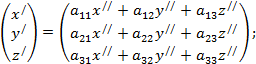
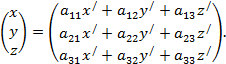
Окончательный результат получится после подстановки значений x^/, y^/, z^/ из верхней формулы в нижнюю и вычисления соответствующих результатов:

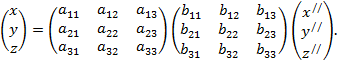
Хотя при умножении матриц переместительный закон неприменим, но сочетательный справедлив. После умножения первых двух матриц можно получить матрицу, которая позволит перевести в

Выражения для x, у, z имеют вид

Коэффициент А₁₁ получится, если элементы первой строки матрицы (а) помножить на элементы первого столбца матрицы (b) и результаты сложить:

Коэффициент A₁₂ получится аналогичным перемножением элементов первой строки матрицы (а) на соответствующие элементы второго столбца матрицы (b):

Коэффициент A₁₃ получится из элементов первой строки матрицы (а) и элементов третьего столбца матрицы (b):

Для получения коэффициентов А₂₁, А₂₂, A₂₃ в выражении для у надо элементы второй строки матрицы (а) умножить соответственно на элементы первого, второго и третьего столбцов матрицы (b):

Аналогично делается и с коэффициентами в выражении для z:

Если элементы каждого столбца и строки рассматривать как скаляры, определяющие некоторый вектор, то в выражении для х коэффициенты при x^//, y^//, z^// можно получить скалярным умножением вектора первой строки матрицы множимого на векторы первого, второго и третьего столбцов матрицы множителя.

Это правило можно применять и при умножении неквадратных матриц, но только если число строк множимого равняется числу столбцов множителя; матрица, получающаяся после произведения, имеет такую же структуру, как и матрица множимого.

Рассмотрим теперь подробнее матрицы, которые представляют вращение.

Пусть Оху — некоторая система координат, а Ох^/у^/ — другая система, получившаяся из первой в результате поворота ее вокруг О на угол φ против вращения часовой стрелки.

Формулы преобразования координат:

Это преобразование при помощи матриц можно представить в виде

Если в пространстве трех измерений рассматривать вращение вокруг оси Оz, то, поскольку z^/ = z, соответствующую матрицу можно изобразить так:

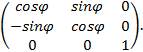
При помощи матриц можно вывести кинематические формулы Эйлера, выражающие связь между проекциями угловых скоростей на подвижные и неподвижные оси.

Рассмотрим матрицу, определяющую общий случай вращения с угловой скоростью:

Линейная скорость точки с радиусом-вектором

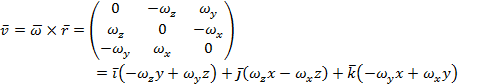
есть выражение, которое получается после разложения детерминанты по элементам верхней строки. Результат можно представить в таком виде:

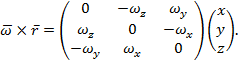
Первый множитель представляет оператор, выражающий вращение с угловой скоростью. Полученная матрица имеет элементы главной диагонали, равные нулю. Если рассматривать диагональ как некоторую ось симметрии, то соответствующие элементы имеют противоположные знаки. Такая матрица называется антиметрической. Эта антисимметричность характерна для операторов, представляющих вращение, что следует из выражений, приведенных выше, для изображения вращений вокруг координатных осей.

Рассмотрим теперь оператор, соответствующий простейшему случаю чистой деформации без вращения — деформации сжатия или растяжения — по трем взаимно перпендикулярным направлениям:

Соответствующая матрица имеет вид

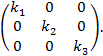
Ее элементы, симметрично расположенные относительно главной диагонали, равны. Такие матрицы называются кососимметрическими. Как видно, самое общее преобразование (без поступательной части) можно разложить на два преобразования: вращение в чистую деформацию.

Первоначально определим сумму матриц.

Если имеются две матрицы с одинаковыми числами строк и столбцов, то эти матрицы можно сложить; их сумма выражается такой же матрицей, каждый элемент которой равен сумме соответствующих элементов складываемых матриц.

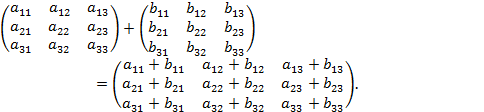
Пусть теперь дана матрица

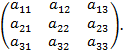
Составим выражения

Тогда

Поэтому

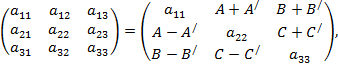
что можно представить в виде суммы двух матриц:

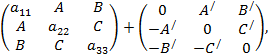
из которых левая является кососимметрической, а правая — антиметрической.

Так как по закону Гука деформации прямо пропорциональны напряжениям, то при помощи матриц можно перейти и к исследованию распределения напряжений в упругих средах.

Возьмем в начале координат бесконечно малый объем упругого вещества, имеющий форму тетраэдра, три грани которого лежат на плоскостях координат; пусть нормаль к четвертой грани образует с координатными осями Ох, Оу, Oz (рис. 39) углы α, β, γ.Составим уравнения равновесия этого объема, учитывая лишь действия на последний упругих сил, величины которых пропорциональны поверхности граней.

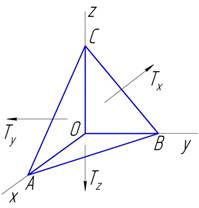
Рис. 39

Пусть dS — площадь грани ABC; площади трех остальных граней, представляющих проекции dS на перпендикулярные плоскости, соответственно dS cosα, dS cosβ, dS cosγ. Пусть на грани действуют упругие напряжения Т_х, Т_у, T_z, Т_s, направления которых не перпендикулярны граням.

Условие, выражающее равенство нулю суммы упругих сил, приложенных к тетраэдру, представится в виде

откуда

Это выражение аналогично проекции силы на направление единичного вектора :

но только вместо скаляров Р_x, Р_у, Р_z имеются векторы. Если сила определяется тремя скалярными проекциями, то величина рассматриваемом случае определяется тремя векторами , , такие величины называются тензорами. Первым примером таких величин были физические «силы», определяющие напряженное состояние упругого тела.

Попробуем найти выражение для этой величины, аналогичное тому, которое определяет вектор при помощи трех скаляров проекций.

Разложим векторы , , Тг по координатйым осям:

Величины T_хх,T_уу, Т_zz представляют нормальные напряжения, действующие на соответствующие грани; условимся считать их положительными, если они являются растягивающими, и отрицательными, если они производят сжатие. Остальные шесть величин — векторы напряжений, действующих в плоскостях граней; они аналогичны срезывающим усилиям в «Сопротивлении материалов».

Можно показать, что эти шесть усилий сводятся к трем, а именно:

Так как приложенные к тетраэдру силы считаем направленными во внешнюю сторону от рассматриваемого объема, то проекции T_хх,T_уу, Т_zz отрицательны и получаем

аналогично и для других величин. Выражение для примет вид

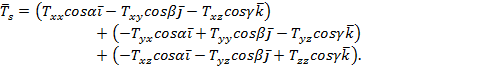
Это выражение можно представить в виде матрицы, состоящей из одного столбца:

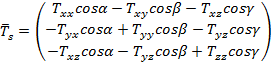
или в виде произведения двух матриц:

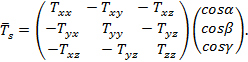
Выражение вектора _S представляющее упругое напряжение, действующее на площадку, ориентация которой определяется направляющими косинусами cosα, cosβ, cosγ, рассматривается матричное произведение некоторой матрицы на вектор =cosα+cosβ+cosγ единичного вектора нормали. Оно вполне аналогично выражению, определяющему проекцию силы на вектор ,

т.е. , но только в рассматриваемом случае вместо вектора имеется кососимметричная матрица:

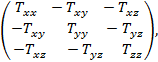
которая представляет тензор напряжений для рассматриваемой точки упругой среды. В данной точке можно провести любое количество площадок с различными ориентациями; умножая тензор напряжений на единичный вектор ориентации, получаем векторное выражение силы, действующей в этой точке на помещенную в ней площадку с соответствующей ориентацией.

Теперь определим величину нормального напряжения, действующего на заданную площадку; для этого нужно взять проекцию силы _S на единичный вектор ориентации =cosα+cosβ+cosγk; тогда

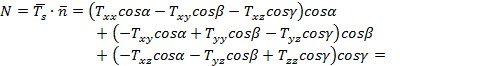
Сравним теперь полученное выражение с формулой, которую получаем по теореме о шести постоянных для величины момента инерции тела относительно оси с направляющими косинусами cos α, cos β, cos γ:

Одинаковость полученных выражений позволяет представить выражение для в том же виде, какой получен для нормального напряжения N:

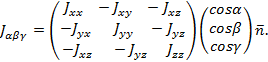
Стоящая в этой формуле кососимметрическая матрица носит название тензора инерции.

Введение тензора инерции позволяет упростить формулы, встречающиеся в динамике твердого тела. Так, в простейшем случае вращения твердого тела вокруг неподвижной оси кинетический момент тела вокруг этой оси равняется произведению тензора инерции J на угловую скорость ω. Кинетический момент относительно точки, лежащей на оси вращения с угловой скоростью

можно представить в виде

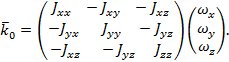
Если координатные оси являются главными, то центробежные моменты инерции равны нулю и тензор инерции имеет вид

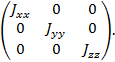
Приведем соответствующее выражение для тензора напряжений:

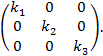
Так получается чистая деформация растяжения или сжатия по трем взаимно перпендикулярным направлениям, и упругие силы Т имеют направления, совпадающие с нормалями к соответствующим площадкам. Соответствующие направления в данной точке совпадают с главными осями инерции для той же точки. Поэтому две, казалось бы, совершенно различные задачи — отыскание направлений главных напряжений и главных осей инерции — сводятся к одной и той же — отысканию направлений главных осей эллипсоида, решение которой дается в любом курсе аналитической геометрии.

Эту часть механики стали называть теорией упругости. Ее создали Пуассон (1781—1840) и великий французский математик Августин Коши (1788—1867). После окончания Политехнической школы, где Коши получил полное инженерное образование, он стал читать лекции в College de France. Значение его как математика огромно: он первый приступил к упорядочению высшего анализа, который в XVIII в. разрабатывался чисто практически, не обращая внимания на теоретическое обоснование. Он является основателем теории функций мнимого переменного. В механике сплошной среды непрерывную материю он заменил непрерывными геометрическими переменными.

Основной работой Пуассона в области теории упругости является его «Мемуар об общих уравнениях равновесия и движения твердых упругих тел и жидкостей». Пуассон в науке продолжал традиции Лапласа. Кроме курса теоретической механики, написанного по схеме Лапласа, ему принадлежат два мемуара по притяжению эллипсоидов. Он занимался теорией упругости; в частности, напирал работу о колебании бесконечно тонких пластинок и большой мемуар «О равновесии и движении упругих твердых тел и жидкостей», изложенный с точки зрения молекулярной механики: молекулы всех тел взаимно притягиваются и вместе с тем отталкиваются вследствие действия теплоты; сила взаимодействия двух молекул есть еще неизвестная функция расстояния, отличная от нуля в «радиусе действия» молекулы и быстро убывающая при значительных величинах расстояния. Он продолжал работы Лапласа в теории капиллярных явлений, а также в математической теории тяготения. В теории поля он распространил исследования и на область электростатических и магнитных явлений.

С исторической точки зрения интересна его полемика о волновой теории света, созданной Френелем. Начало этой полемики восходит еще к Лапласу, придерживавшемуся ньютоновской теории истечения и давшему теорию, объяснявшую законы распространения света в прозрачных телах с точки зрения движения световых частиц. Пуассон продолжил эту полемику и показал, что при справедливости теории Френеля средняя точка тени от весьма малых тел должна быть так же освещена, как при отсутствии затемняющего тела. Френель поставил соответствующий опыт, который показал, что явление, предсказанное теорией Пуассона, действительно имеется. Таким образом, опровержение волновой теории, которое Пуассон считал решающим, обратилось в блистательное ее подтверждение. Учеником Пуассона был М. В. Остроградский.

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00