Главная

Лекция 6. Кинетическая энергия системы.

В данной лекции рассматриваются следующие вопросы:

1. Кинетическая энергия системы. Теорема Кенига.

2. Некоторые случаи вычисления работы.

3. Теорема об изменении кинетической энергии системы.

4. Закон сохранения механической энергии.

5. Методические указания по решению задач с применением законов сохранения.

Изучение данных вопросов необходимо для динамики колебательного движения механической системы, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Кинетическая энергия системы.

Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы

Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.

Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:

Кинетическая энергия – скалярная и всегда положительная величина.

Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки V_i=V_C

или

Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.1), то скорость любой его точки где - расстояние точки от оси вращения, а - угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:

Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:

т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.

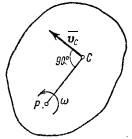
Рис.1

При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.2)

или, окончательно,

где – моменты инерции тела относительно главных осей инерции x₁, y₁, z₁ в неподвижной точке О; – проекции вектора мгновенной угловой скорости на эти оси.

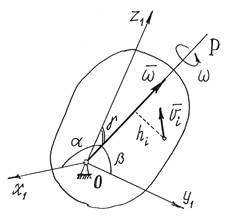
Рис.2

3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис.1). Следовательно

где - момент инерции тела относительно названной выше оси, - угловая скорость тела. Величина в формуле будет переменной, так как положение центра Р при движении тела все время меняется. Введем вместо постоянный момент инерции, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса-Штейнера , где d=PC. Подставим это выражение для. Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно, , где - скорость центра масс С, окончательно найдем:

Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.

4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.

Рассмотрим движение материальной системы как сумму двух движений (рис.3). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x₁, y₁, z_1. Тогда скорость точек . Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны . Значит, и кинетическая энергия будет

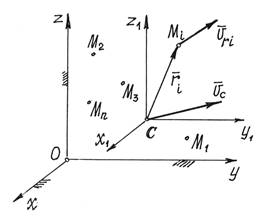
Рис.3

По определению центра масс его радиус-вектор в подвижной системе (центр масс находится в начале координат), значит, и . Производная по времени от этой суммы также равна нулю:

Поэтому, окончательно, кинетическая энергия системы

Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс.

В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим

где I_x, I_y, I_z – главные центральные оси инерции тела.

Некоторые случаи вычисления работы.

1) Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу весом , будет равна , где и - координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна

где Р - вес системы, - вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей Р на перемещении центра тяжести (или центра масс) системы.

2) Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.4) будет равна

,

так как где - угол поворота тела.

Но, как легко видеть, . Будем называть величину вращающим моментом. Тогда получим: .

Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать .

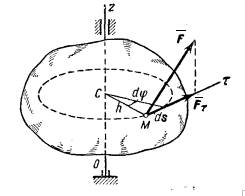
Рис.4

При повороте на конечный угол работа будет равна

а в случае постоянного момента (M_z=const)

Рисунок 27

Если на тело действует пара сил, лежащая в плоскости, перпендикулярной к оси Оz, то Мz будет, очевидно, означать момент этой пары.

Работа, затрачиваемая на изменение скорости вращения, равна изменению кинетической энергии тела:

Укажем еще, как в данном случае определяется мощность

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощности вращающий момент будет тем больше, чем меньше угловая скорость.

Если тело катится по горизонтальной поверхности, его кинетическая энергия будет складываться из энергии поступательного движения и энергии вращения (рис.5):

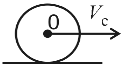
Рис.5

3) Работа сил трения, действующих на катящееся тело. На колесо радиуса R (рис.6), катящееся по некоторой плоскости (поверхности) без скольжения, действует сила трения F , препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы . Но точка В в данном случае является мгновенным центром скоростей и V_B=0. Так как , то и для каждого элементарного перемещения dA=0.

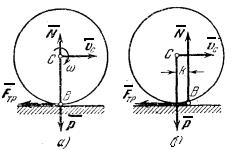
Рис.6

Следовательно, при качении без скольжения, работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю. По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.6,а).

Сопротивление качению, возникающее вследствие деформации поверхностей (pис.6,б), создает пару (), момент которой M=kN, где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса , получим:

где - элементарное перемещение центра С колеса.

Если N= const, то полная работа сил сопротивления качению будет равна

Так как величина k/R мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.

Пример 1. Шар массой m =1 кг катится без скольжения по горизонтальной плоскости со скоростью v=2 м/с. Найти кинетическую энергию шара.

Решение. Кинетическая энергия шара в случае качения без скольжения складывается из кинетической энергии поступательного движения центра масс шара и кинетической энергии его вращательного движения, т.е.

Поскольку момент инерции шара , а , то

Пример 2. С какой наименьшей высоты должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом R = 3 м и не сорваться в верхней точке петли (рис.7)? Масса велосипедиста с велосипедом m = 75 кг, причем на колеса приходится масса m₀= 3 кг. Колеса велосипеда считать обручами.

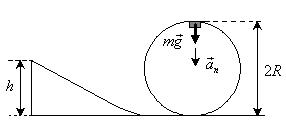
Рис.7

Решение. На вершине наклонной плоскости велосипедист обладает потенциальной энергией W_П=mgh. По закону сохранения энергии этой энергии должно хватить на подъем на высоту 2R () и на движение со скоростью v. Эту скорость найдем, записав II закон Ньютона для верхней точки «мертвой петли»,

Тогда Откуда . Обратим внимание на то, что кинетическая энергия велосипедиста складывается из кинетической энергии поступательного движения его центра масс и кинетической энергии вращательного движения двух колес его велосипеда, т.е.

Поскольку колеса – обручи массой m₀/2 каждое, то их моменты инерции равны , а кинетическая энергия каждого колеса

Отсюда

Пример 3. Найти линейные скорости и ускорения центров шара, диска и обруча, скатившихся с наклонной плоскости высотой h = 1 м и углом наклона α=30°. Начальная скорость всех тел v₀=0. Сравнить найденные значения со скоростью и ускорением бруска, соскользнувшего с той же наклонной плоскости при отсутствии трения.

Решение. Для всех перечисленных в условии задачи тел закон сохранения энергии записывается в виде W_П=W_k. Различие состоит в том, что для шара, диска и обруча кинетическая энергия

а для бруска

Учитывая, что моменты инерции перечисленных тел запишем:

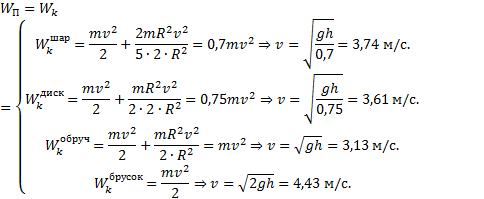
Ускорения найдем, воспользовавшись формулой , где v₀=0, а Тогда

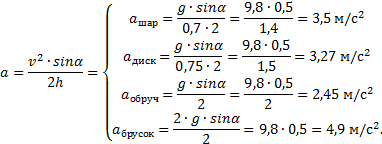
Пример 4. Колесо, вращаясь равнозамедленно, уменьшило за время t=60 сек, частоту вращения с n₁=5 об/с до n₂=3 об/с. Колесо считать тонкостенным обручем массой m=1 кг и радиусом R = 0,2 м. Найти угловое ускорение колеса ε, момент сил торможения M, работу сил торможения А и число оборотов N, сделанных колесом за время t = 60 с.

Решение. Поскольку движение колеса является равнозамедленным, то оно описывается формулами

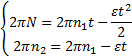
Отсюда модуль углового ускорения

Количество оборотов

Момент инерции обруча I=mR²=1∙0,2²=0,04 кг∙м².

Из основного уравнения динамики вращательного движения

найдем момент сил торможения M=I∙ε=0,04∙0,21=8,4∙10^-3 Н∙м.

Работа сил торможения может быть найдена из соображений, что она пошла на изменение кинетической энергии вращающегося колеса.

Тогда,

Пример 5. Тонкий однородный стержень длиной l может вращаться относительно горизонтальной оси, проходящей через конец стержня (рис.8). Стержень отклонили на 90° от положения равновесия и отпустили. Определить скорость v нижнего конца стержня в момент прохождения положения равновесия.

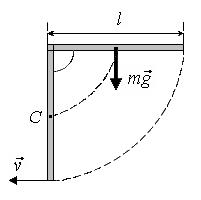
Рис.8

Решение. При движении стержня выполняется закон сохранения энергии W_П=W_k,

где W_П - потенциальная энергия стержня в начальном (поднятом) положении, а W_k - кинетическая энергия в момент прохождения положения равновесия. Обратим внимание на тот факт, что в качестве «нулевого» уровня потенциальной энергии принимается уровень центра масс С стержня в положении равновесия.

Потенциальная энергия W_П=mgl/2.

Поскольку стержень вращается, то его кинетическая энергия

Для нахождения момента инерции I стержня относительно оси, проходящей через его конец, воспользуемся теоремой Штейнера:

Угловая скорость стержня ω=v/l.

Кинетическая энергия

Отсюда

и скорость нижнего конца стержня в момент прохождения положения равновесия

Теорема об изменении кинетической энергии системы.

Если рассмотреть какую-нибудь точку системы с массой , имеющую скорость , то для этой точки будет

где - элементарные работы действующих на точку внешних и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим

или

. (2)

Равенство выражает теорему об изменении кинетической энергии системы в дифференциальной форме.

Если полученное выражение отнести к элементарному промежутку времени, в течение которого произошло рассматриваемое перемещение, можно получить вторую формулировку для дифференциальной формы теоремы: производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних (N^e) и внутренних (N^k) сил, т.е.

Дифференциальными формами теоремы об изменении кинетической энергии можно воспользоваться для составления дифференциальных уравнений движения, но это делается достаточно редко, потому что есть более удобные приемы.

Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна T₀, в положение, где значение кинетической энергии становится равным T₁, будем иметь

Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

В отличие от предыдущих теорем, внутренние силы в уравнениях не исключаются. В самом деле, если и - силы взаимодействия между точками B₁ и B₂ системы (см. рис.6), то . Но при этом точка B₁, может перемещаться по направлению к B₂, а точка B₂- по направлению к B₁. Работа каждой из сил будет тогда положительной и сумма работ нулем не будет. Примером может служить явление отката. Внутренние силы (силы давления), действующие и на снаряд и на откатывающиеся части, совершают здесь положительную работу. Сумма этих работ, не равная нулю, и изменяет кинетическую энергию системы от величины W_k0=0 в начале выстрела до величины W_k1= W_kCHAP+ W_kOTK конце.

Другой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, не упругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.

Все предыдущие теоремы позволяли исключить из уравнений движения внутренние силы, но все внешние силы, в том числе и наперед неизвестные реакции внешних связей, в уравнениях сохранялись. Практическая ценность теоремы об изменении кинетической энергии состоит в том, что при не изменяющихся со временем идеальных связях она позволит исключить из уравнений движения все наперед неизвестные реакции связей.

Теорему об изменении кинетической энергии удобно использовать при решении задач, в которых требуется установить зависимость между скоростями и перемещениями тел.

Рассмотрим два важных частных случая.

1) Неизменяемая система. Неизменяемой будем называть систему, в которой расстояния между точками приложения внутренних сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.

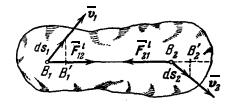
Рис.9

Пусть две точки B₁ и B₂ неизменяемой системы (pис.9), действующие друг на друга с силами и () имеют в данный момент скорости и . Тогда за промежуток времени dt эти точки совершат элементарные перемещения и , направленные вдоль векторов и . Но так как отрезок B₁B₂ является неизменяемым, то по известной теореме кинематики проекции векторов и ,а, следовательно, и перемещений и на направление отрезка B₁B₂ будут равны друг другу, т.е. . Тогда элементарные работы сил и будут одинаковы по модулю и противоположны по знаку и в сумме дадут нуль. Этот результат справедлив для всех внутренних сил при любом перемещении системы.

Отсюда заключаем, что для неизменяемой системы сумма работ всех внутренних сил равна нулю и уравнения принимают вид

2) Система с идеальными связями. Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей. Тогда

где - элементарная работа действующих на k-ю точку системы внешних и внутренних активных сил, a - элементарная работа реакций наложенных на ту же точку внешних и внутренних связей.

Как видим, изменение кинетической энергии системы зависит от работы и активных сил и реакций связей. Однако можно ввести понятие о таких «идеальных» механических системах, у которых наличие связей не влияет на изменение кинетической энергии системы при ее движении. Для таких связей должно, очевидно, выполняться условие:

Если для связей, не изменяющихся со временем, сумма работ всех реакций при элементарном перемещении системы равна нулю, то такие связи называют идеальными. Для механической системы, на которую наложены только не изменяющиеся со временем идеальные связи, будем, очевидно, иметь

Таким образом, изменение кинетической энергии системы с идеальными, не изменяющимися со временем связями при любом ее перемещении равно сумме работ на этом перемещении, приложенных к системе внешних и внутренних активных сил.

Механическая система называется консервативной (энергия ее как бы законсервирована, не изменяется), если для нее имеет место интеграл энергии

W=W_K+W_П=const или . (3)

Это есть закон сохранения механической энергии: при движении системы в потенциальном поле механическая энергия ее (сумма потенциальной и кинетической) все время остается неизменной, постоянной.

Или

В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

Это один из фундаментальных законов природы. Он подтверждает положение материализма о том, что движение является неотъемлемой частью материи, что оно неуничтожимо, а лишь преобразуется из одной формы в другую. Согласно всеобщему закону сохранения и превращения энергии уменьшение или увеличение полной механической энергии системы в точности компенсируется увеличением или уменьшением какого-либо другого вида энергии.

Энергия никуда не исчезает и не появляется вновь, а лишь переходит от одного тела к другому или превращается из одного вида в другой.

Механическая система будет консервативной, если действующие на нее силы потенциальны, например сила тяжести, силы упругости. В консервативных механических системах с помощью интеграла энергии можно проводить проверку правильности составления дифференциальных уравнений движения. Если система консервативна, а условие (3) не выполняется, значит при составлении уравнений движения допущена ошибка.

В замкнутой системе тел, силы взаимодействия в которой консервативные, взаимные превращения механической энергии в другие виды отсутствуют. Такие системы называются замкнутыми консервативными системами.

Интегралом энергии можно воспользоваться для проверки правильности составления уравнений и другим способом, без вычисления производной. Для этого следует после проведения численного интегрирования уравнений движения вычислить значение полной механической энергии для двух различных моментов времени, например, начального и конечного. Если разница значений окажется сопоставимой с погрешностями вычислений, это будет свидетельствовать о правильности используемых уравнений.

Методические указания по решению задач с применением законов сохранения.

Приведем содержание метода применения законов изменения и сохранения энергии, импульса и момента импульса в виде предписания алгоритмического типа.

1. Выяснить, какие процессы описаны в условии задачи. Для каждого процесса ввести обозначения параметров начального и конечного состояний. Последующие операции алгоритма выполнять для каждого процесса.

2. Указать, какие тела включаем в систему тел.

3. Выбрать систему отсчета - инерциальную или неинерциальную.

4. Установить силы, действующие на каждое тело системы, при переходе из одного состояния в другое. Провести анализ сил, выделив внешние и внутренние, потенциальные и диссипативные.

5. Установить, какой закон следует применять при решении данной задачи. Для этого произвести анализ правой части в выражениях (1), (2), (4), (6).

6. Если энергия, импульс или момент импульса изменяются при рассматриваемом процессе, записать выражения для работы, импульса силы, импульса момента силы.

7. Записать выражения для энергии, импульса или момента импульса каждого тела в отдельности и всей системы в начальном и конечном состояниях.

8. Применить соответствующие законы для каждого процесса.

9. Если необходимо, установить уравнения кинематической связи.

10. Проверить, является ли система уравнений полной, решить ее в общем виде.

11. Проанализировать полученный результат.

Примечания: В приведенных ниже примерах решения задач

- не акцентируется внимание на выполнении пункта 1, если происходит один процесс;

- не обсуждается вопрос о выборе системы отсчета, если рассматривается движение относительно Земли (инерциальной системы отсчета);

- не затрагивается вопрос о характере взаимодействия тел системы, если подобный анализ производился в предыдущих задачах.

Пример 6. Какую скорость надо сообщить точке М стержня, прикрепленного верхним концом с помощью шарнира О к неподвижной поверхности (рис.10), чтобы стержень совершил четверть оборота?

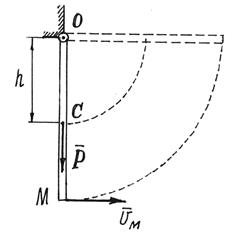
Рис.10

Решение. В первом, вертикальном, положении кинетическая энергия стержня, начавшего вращаться вокруг оси О,

Во втором положении, где стержень достигнет горизонтального положения и остановится на мгновение, Т₂ = 0.

Работу совершит только вес стержня Р: A=-Ph=-Pl/2. По теореме получим уравнение , из которого следует .

Пример 7. Механическая система состоит из двух шаров A и B, связанных с шарниром O и ползуном C невесомыми стержнями (рис.11).

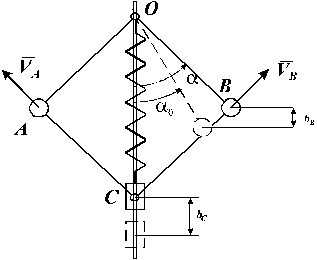
Рис.11

Массы шаров и ползуна одинаковы и равны m=0,2 кг. Стержни имеют одинаковую длину l= 0,3 м. Между шарниром и ползуном установлена пружина жесткостью c =100 Н/м, длина которой в недеформированном состоянии равна l (рис.8). Требуется определить зависимость скоростей движения шаров от угла отклонения стержней от вертикали и найти максимальное отклонение, если в начальный момент времени система покоилась, а угол составлял .

Решение. Кинетическая энергия системы складывается из кинетических энергий трех тел, которые по условию могут рассматриваться как материальные точки.

Скорости шаров пропорциональны угловой скорости вращения стержней OA и OB

Скорость ползуна нетрудно определить, если учесть, что

.

Тогда

Подставляя выражения для скоростей в (4), получим зависимость кинетической энергии системы от скоростей шаров V и угла отклонения стержней

(5)

Определим работу, которую совершат все силы, приложенные к системе при ее перемещении из начального положения в конечное. Работа сил тяжести определяется вертикальными перемещениями центров тяжести тел (см. рис.8):

Для вычисления работы силы упругости воспользуемся формулой:

Подставляя выражения (5), (6) и (7) в уравнение теоремы об изменении кинетической энергии, получаем зависимость скорости движения шаров от угла

или в явном виде

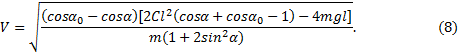
Если в уравнении 8 скорость V приравнять нулю, можно найти два предельных значения угла , между которыми будет происходить движение системы при заданным начальных условиях:

Пример 8. С наклонной плоскости высотой h=1 м и длиною склона l=10 м скользит тело массой в m=1 кг. Найти: 1) кинетическую энергию тела W_k у основания плоскости, 2) скорость тела v у основания плоскости, 3) расстояние s, пройденное телом по горизонтальной части пути до остановки. Коэффициент трения на всем пути считать постоянным и равным 0,05.

Решение. Потенциальная энергия тела при скольжении его с наклонной плоскости переходит в кинетическую энергию и в работу против силы трения, т.е. mgh=mv²/2 + F_трl. Но h=lsina, F_тр=𝜇mg∙cosα, где α - угол наклона плоскости.

1) W_k= mv²/2=mgh- F_трl =mgl(sinα – μcosα). У нас sinα=h/l=0,1, т.е. α=5°44’, следовательно, cosα=0,995.

Подставляя числовые данные задачи, получим W_k=4,9 Дж.

2)

3) Кинетическая энергия тела у основания наклонной плоскости переходит в работу против сил трения на горизонтальной части пути, т.е.

W_k=F_тр∙s =μmgs, откуда s=W_k/μmg=10 м.

Пример 9. Два тела с массами m и 3m движутся во взаимно перпендикулярных направлениях (см.рис.12). После соударения тело массы m остановилось . Какую часть его энергии составляет выделившееся при ударе тепло Q/Е_к1?

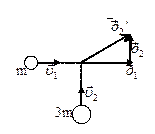
Рис.12

Решение. Так как время соударения мало, то суммарный импульс системы не изменяется.

где Но , т.к. , поэтому .

Из рисунка видно, что

Кинетическая энергия тел до столкновения

Кинетическая энергия тела с массой 3m после столкновения

Убыль кинетической энергии означает, что ее часть превратилась во внутреннюю энергию тела, т.е.

Тогда

т.е. 2/3 кинетической энергии первого тела превратилось в тепло.

Пример 10. Сваю массой m₂=100 кг забивают в грунт копром, масса которого m₁=300 кг. Копер свободно падает с высоты H=4 м и при каждом ударе опускается на h=10 см=0,1 м. Определить силу сопротивления грунта F_c, считая ее постоянной, а удар копра о сваю абсолютно неупругим.

Решение. При падении копра его потенциальная энергия превращается в кинетическую: . Тогда скорость копра в момент удара о сваю v₁=(2gh)^1/2. Удар о сваю неупругий. По закону сохранения импульса m₁v₁=(m₁+m₂)∙v₂. Отсюда v₂=m₁v₁/(m₁+m₂). При движении сваи в грунт действует сила сопротивления, т.е. система незамкнута, поэтому изменение полной энергии системы: ∆Е=А_Fc;

где А_Fc=-F_c∙h - работа силы сопротивления.

Тогда

F_c=94∙10³ H=94 кН.

Пример 11. Груз массой m₁=0,5 кг падает с некоторой высоту на плиту массой m₂=1 кг, укрепленную на пружине жесткостью k=9,8∙10² Н/м. Определить наибольшее сжатие пружины x, если в момент удара груз обладал скоростью v₁=5 м/с. Удар неупругий.

Решение. Так как в системе действуют только силы тяжести и упругости, то система является замкнутой и выполняется закон сохранения энергии. Полная механическая энергия груза вместе с плитой после удара равна потенциальной энергии сжатой пружины:

где v₂ - скорость груза и плиты после удара, которую найдем по закону сохранения импульса: m₁v₁=(m₁+m₂)∙v₂.

Откуда

Подставим это выражение в (1):

Решая это уравнение, получим х=8,2∙10^-2 м=8,2 см.

Пример 12. Груз массой m=1 кг, висящий на нити, отклоняют на угол α=30° (рис.13). Найти натяжение нити F_н в момент прохождения грузом положения равновесия.

Рис.13

Решение. Натяжение нити в момент прохождения маятником положения равновесия

Кроме того, по закону сохранения энергии , откуда .

Но из рис.13 h=l - lcosα= l(1-cosα).

Тогда

и F_н=mg[1+2 mg(1-cosα)]=12,4 H.

Пример 13. С горки с одной и той же высоты а) соскальзывает без трения брусок, б) скатывается без проскальзывания сплошной цилиндр. Сравните их скорости у основания горки.

Рис.14

Решение. а) Рассмотрим движение бруска. В состоянии I брусок обладал потенциальной энергией (рис.14)

в состоянии II - кинетической энергией поступательного движения

По закону сохранения энергии W_I=W_II получим

откуда скорость бруска равна

б) Рассмотрим движение цилиндра. В состоянии I цилиндр обладал потенциальной энергией (рис.14)

в состоянии II - кинетической. Однако, в отличие от предыдущего случая цилиндр участвует в двух движениях: поступательном перемещении со скоростью, равной скорости центра масс v_c и вращательном движении вокруг оси, проходящей через центр масс, с угловой скоростью ω. Поэтому полная кинетическая энергия цилиндра состоит из двух частей:

Момент инерции сплошного однородного цилиндра равен , уравнение, связывающее скорости центра масс и угловую скорость имеет вид . Поэтому

Применяя закон сохранения энергии W_I=W_II получим

откуда скорость цилиндра равна

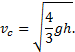
Видно, что

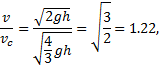
т.е. скорость бруска больше скорости цилиндра в 1,22 раза.

Пример 14. Два одинаковых бруска массой m каждый, соединенные пружиной жесткости k, лежат на горизонтальной плоскости (рис.15). Левый брусок касается вертикальной стенки. Какую минимальную скорость, направленную к стенке, надо сообщить правому бруску, чтобы при обратном движении от стенки он сдвинул левый брусок? Коэффициент трения каждого бруска о плоскость равен μ. Пружина в начальный момент не деформирована.

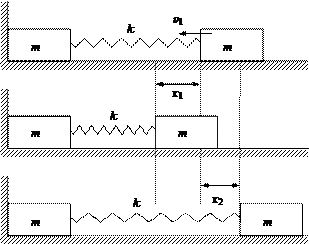
Рис.15

Решение. На каждый из брусков действуют вертикальные силы тяжести mg и нормального давления N, а также горизонтальные силы упругости со стороны деформированной пружины F и трения F_тр.

Рассмотрим следующие состояния системы тел “бруски + пружина”.

I. В начальном состоянии скорость правого бруска равна v₁, пружина не деформирована.

II. Правый брусок сместился на x₁, его скорость уменьшилась до нуля, пружина сжата и действует на бруски с силой упругости Вследствие действия этой силы правый брусок начинает двигаться в противоположном направлении, проходит первоначальное положение и растягивает пружину. Если сила упругости превышает максимальную силу трения покоя действующую на левый брусок, последний приходит в движение.

III. Третье состояние соответствует началу движения левого бруска, когда пружина растянулась на x₂. Поскольку в условии задачи требуется найти минимальную скорость v₁, позволяющую сдвинуть левый брусок, в данном состоянии скорость правого бруска равна нулю.

Опишем происходящие в системе процессы.

Условие начала движения левого бруска (рис.16) имеет вид или

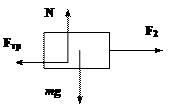
Рис.16

Рассмотрим переход правого бруска из состояния I в состояние II (рис.17). Применим теорему о кинетической энергии, согласно которой ее изменение определяется суммарной работой всех сил, действующих на тело:

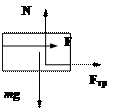
Рис.17

Кинетическая энергия в начальном состоянии , в конечном . Работа силы трения: ; работа силы упругости равна изменению потенциальной энергии со знаком “минус”: ; силы тяжести и нормального давления работы не совершают, поскольку они перпендикулярны направлению перемещения. Тогда выражение (2) примет вид

Аналогично описывается переход правого бруска из состояния II в состояние III. На основе теоремы о кинетической энергии имеем

Кинетическая энергия, как в начальном состоянии, так и в конечном, равна нулю. Работа силы трения

Работа силы упругости

Теорема о кинетической энергии (3) примет вид

или, после сокращения на (x₁+x₂),

Выразим из системы уравнений v₁. Из (1) найдем Подставляя его в (3а), получим

Наконец, с помощью уравнения (2а) приходим к окончательному результату:

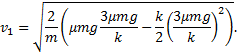
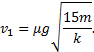
Пример 15. Карандаш длиной l, поставленный вертикально, падает на стол (рис.18). Какую угловую и линейную скорость будут иметь в конце падения середина и верхний конец карандаша?

Рис.18

Решение. На карандаш в процессе движения действуют силы тяжести mg, нормального давления N и трения покоя F_тр. Моменты сил нормального давления и трения относительно оси вращения О равны нулю, сила тяжести - потенциальная сила. Следовательно, можно применить закон сохранения энергии.

В начальном состоянии карандаш обладает потенциальной энергией

где h=l/2 - высота, на которой расположен центр масс С.

В конечном состоянии энергия карандаша является кинетической, выражение для которой при вращательном движении имеет вид:

где J - момент инерции тонкого стержня относительно оси, проходящей через его конец, ; ω - угловая скорость.

Закон сохранения энергии W_II=W_I принимает вид:

Из полученного уравнения нетрудно выразить угловую скорость карандаша непосредственно перед касанием:

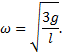
Учитывая связь между линейной и угловой скоростями при вращательном движении по окружности радиуса R: v=ωR, найдем скорости точек А и С:

Пример 13. Доска веса P положена на два катка веса Q каждый. На доску действует постоянная сила F, составляющая с горизонтом угол (рис.19). Катки являются однородными дисками, а проскальзывания катков с доской и с горизонтальной плоскостью нет. В начальный момент времени система покоились. Определить ускорение доски.

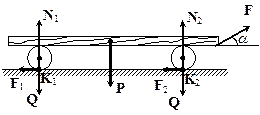
Рис.19

Решение. Исследуемой механической системой в данной задаче является доска вместе с катками. Для решения задачи применим теорему об изменении кинетической энергии: . В качестве W_k2 и W_k1 возьмем значения кинетической энергии системы в произвольный момент времени T₂=T(t) и в начальный момент времени T₁=T(t). По условию задачи в начальный момент времени система покоилась, поэтому T(0)=0. Кинетическая энергия в момент времени t складывается из кинетической энергии доски W_kd и двух катков 2W_kk: W_k(t)= W_kd+2W_kk. Так как доска движется поступательно, то W_kd=PV²/2g. Каждый из катков совершает плоское движение, поэтому, согласно теореме Кенига,

где V_c – скорость оси катка, – угловая скорость его вращения, а I_c – момент инерции катка относительно его оси. Так как каток является однородным диском, то I_c=Qr²/2g, где r – радиус катка. Учитывая теперь условие отсутствия проскальзывания катков с доской и с плоскостью, выпишем кинематические соотношения, связывающие V, V_c и : V = 2V_c, . Следовательно, , и тогда W_k(t)=(8P+3Q)V²/16g.

Вычислим теперь работу всех внешних и внутренних сил за интервал времени от 0 до t. Так как система состоит из абсолютно твердых тел и при этом проскальзывание между доской и катками отсутствует, то сумма работ всех внутренних сил . Внешними силами, действующими на систему, являются силы тяжести доски P и катков Q, постоянная сила F, нормальные реакции плоскости N₁ и N₂ и силы трения между катками и плоскостью F₁ и F₂, приложенные в точках контакта K₁ и K₂ катков (см. рис. 19). Из всех сил работу совершает только сила F, т.е. , где S – перемещение доски за время . Действительно, силы тяжести работу не совершают, так как перемещения точек приложения этих сил перпендикулярны их направлениям. Нормальные же реакции N₁, N₂ и силы трения F₁, F₂ работу не совершают, так как они приложены к мгновенным центрам скоростей K₁ и K₂ катков (в силу отсутствия проскальзывания между катками и плоскостью). Поэтому элементарные перемещения этих точек равны нулю , тем самым равна нулю и элементарная работа указанных сил. Следовательно, равна нулю и суммарная их работа за время от 0 до .

Таким образом, теорема об изменении кинетической энергии в данном случае имеет вид

Для определения ускорения доски a продифференцируем равенство (1) по времени

Учитывая теперь, что и сокращая последнее равенство на общий множитель V, окончательно получаем

Вопросы для самопроверки

- Что называют кинетической энергией материальной точки?

- Что называется кинетической энергией механической системы? Какова ее размерность?

- Выражение кинетической энергии при поступательном, вращательном и плоскопараллельном движении этого тела.

- В каком случае в уравнение теоремы об изменении кинетической энергии не входят внутренние силы этой системы?

- Сформулируйте теорему об изменении кинетической энергии материальной точки в относительном движении. Почему равна нулю работа кориолисовой силы инерции?

- Что называют элементарной работой силы и как она вычисляется?

- Как вычисляется работа силы на конечном пути?

- Как вычисляется работа силы тяжести, силы упругости? Напишите соответствующие формулы.

- Какова сумма работ внутренних сил твердого тела на любом перемещении тела?

- Как вычисляется сумма элементарных работ внешних сил, приложенных к твердому телу: а) в случае поступательного движения; б) в случае его вращения вокруг неподвижной оси; в) в общем случае его движения?

- Сформулируйте теорему об изменении кинетической энергии системы в дифференциальной форме.

- Запишите формулу, выражающую теорему об изменении кинетической энергии системы в интегральной форме.

- Для какой системы изменение кинетической энергии не зависит от внутренних сил?

- Как вычисляется мощность сил, приложенных к твердому телу вращающемуся вокруг неподвижной оси с угловой скоростью ?

- Сформулируйте теорему Кенига о кинетической энергии механической системы в общем случае ее движения.

- Закон сохранения энергии:

1) энергия никогда не исчезает и не появляется вновь, она превращается из одного вида в другой

2) энергия никогда не исчезает

3) уменьшение кинетической энергии равно увеличению потенциальной энергии

4) механическая энергия переходит в энергию теплового движения молекул

5) механическая энергия сохраняется во всех процессах

- Кинетическая энергия вращающегося твердого тела, закрепленного на оси:

1)

2)

3)

4)

5)

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00