Главная

Лекция 1. Динамика точки.

В данной лекции рассматриваются следующие вопросы:

1. Динамика точки.

2. Основные понятия и определения.

3. Законы динамики.

4. Силы в природе.

5. Силы трения.

6. Задачи динамики для свободной и несвободной материальной точки.

7. Методические указания по решению задач.

8. Дифференциальные уравнения движения точи.

9. Движение точки, брошенной под углом к горизонту в однородном поле тяжести.

10. Относительное движение материальной точки.

11. Влияние вращения Земли на равновесие и движение тел.

12. Общие теоремы динамики точки.

13. Количество движения (импульс).

14. Импульс силы.

15. Теорема об изменении количества движения (импульса) точки.

Изучение данных вопросов необходимо для динамики движения центра масс механической системы, динамики вращательного движения твердого тела, кинетического момента механической системы, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Динамика точки. Основные понятия и определения.

В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.

В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.

Понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоянными. Между тем, на движущееся тело наряду с постоянными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.

Сила – векторная физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть появляется ускорение, или происходит деформация тела, либо имеет место и то, и другое. В том случае, когда тело при взаимодействии получает ускорение, говорят о динамическом проявлении сил. В том случае, когда тело при взаимодействии деформируется, говорят о статическом проявлении сил. – векторная величина.

Как показывает опыт, переменные силы могут определенным образом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха).

К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.

Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.

Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

За единицу массы принят эталон – сплав платины и иридия, хранящийся в палате мер и весов в Париже: [m]=кг. Масса–величина аддитивная и скалярная.

В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т.е. от распределения масс).

Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния формы тел (распределения масс), вводится понятие о материальной точке.

Под материальной точкой понимают материальное тело столь малых размеров, что различием в движении отдельных его точек можно пренебречь и положение которого можно определить координатами одной из его точек.

Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.

Наконец, материальными точками можно считать частицы, на которые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.

Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.

При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.

Поэтому при изучении динамики выделяют два основных раздела: "Динамика материальной точки" и "Динамика материальной системы", из которых первый предваряет второй.

Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.

Законы динамики

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.

Первый закон (закон инерции), открытый Галилеем, гласит: существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано.

или в другой формулировке

если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое.

Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоянной по модулю и направлению скоростью ( =const); ускорение точки при этом равно нулю: = 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.

Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). По данным опыта для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.

Системы отсчета, в которых не выполняется первый закон Ньютона, называются неинерциальными. Неинерциальными будут системы, движущиеся с ускорением, или вращающиеся.

Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы (рис.1).

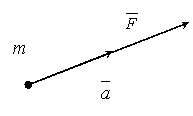
Рис.1

Математически этот закон выражается векторным равенством .

При этом между модулями ускорения и силы имеет место зависимость ma = F.

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.

Известно, что вес тела и ускорение его свободного падения пустоте существенно зависят от места земной поверхности. В данной точке земли ускорение свободного падения всех тел одинаково и обозначается буквой g. Экспериментально установлено, что отношение веса Р тела к ускорению его свободного падения g есть постоянная величина, не зависящая от места наблюдения. Это отношение m = P/g также определяет массу тела. Таким образом, различают тяжелую массу m₁ = P/g и инертную массу m₂ = F/a. В классической механике считается, что m₁=m₂=m.

Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействующей , равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид

или .

Существует и более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равно действующей на нее силе: . Данное выражение называется уравнением движения материальной точки.

В общем случае сила, действующая на тело, изменяется со временем и по величине, и по направлению. Но в течение элементарного промежутка времени dt мы можем считать, что =const. Векторная величина , равная , называется элементарным импульсом (силы).

Второй закон Ньютона в дифференциальной форме:

в проекциях на оси:

Из второго закона также получим размерность силы: 1Н=1 кг∙1 м/с².

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны (рис.2).

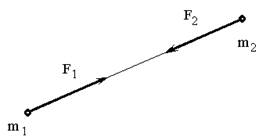
Рис.2

Заметим, что силы взаимодействия между свободными материальными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.

Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе , той, которую мы прикладываем к нему.

Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки - . По третьему закону она равна и противоположна действующей на точку силе, . Но на основании второй аксиомы . Поэтому .

Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение

F^ин=ma.

И направлена эта сила инерции в сторону противоположную вектору ускорения.

Например, при движении точки по кривой линии ускорение . Поэтому сила инерции

.

То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.

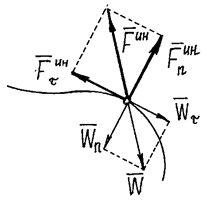
Рис.3

Причём

Необходимо заметить, что сила инерции материальной точки, как сила противодействия, приложена не к точке, а к тому телу, которое изменяет её движение. Это очень важно помнить.

Третий закон динамики, как устанавливающий характер взаимодействия материальных частиц, играет большую роль в динамике системы.

Четвертый закон (закон независимого действия сил). При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

Законы Ньютона в классической механике применимы для описания движения: а) макротел; б) для тел постоянной массы; в) при скоростях, значительно меньших скорости света.

Силы в природе.

В природе существует много разных видов сил: тяготения, тяжести, Лоренца, Ампера, взаимодействия неподвижных зарядов и т.д., но все они в конечном счете сводятся к небольшому числу фундаментальных (основных) взаимодействий. Современная физика считает, что существует в природе лишь четыре вида сил или четыре вида взаимодействий:

1) гравитационное взаимодействие (осуществляется через гравитационные поля);

2) электромагнитное взаимодействие (осуществляется через электромагнитные поля);

3) ядерное (или сильное) (обеспечивает связь частиц в ядре);

4) слабое (отвечает за процессы распада элементарных частиц).

В рамках классической механики имеют дело с гравитационными и электромагнитными силами, а также с упругими силами и силами трения.

Гравитационные силы (силы тяготения) – это силы притяжения, которые подчиняются закону всемирного тяготения.

Сила тяжести – сила, с которой тело притягивается Землей. Под действием силы притяжения к Земле все тела падают с одинаковым относительно поверхности Земли ускорением , называемым ускорением свободного падения. По второму закону Ньютона, на всякое тело действует сила: , называемая силой тяжести.

Вес – сила, с которой тело, притягиваясь к Земле, действует на подвес или опору.

Сила тяжести равна весу только в том случае, когда опора или подвес неподвижны относительно Земли. По модулю вес может быть как больше, так и меньше силы тяжести . Эти силы приложены к разным телам: – приложена к самому телу, – к подвесу или опоре, ограничивающим свободное движение тела в поле земного тяготения.

В случае ускоренного движения опоры (например, лифта, везущего груз) уравнение движения (с учетом того, что сила реакции опоры равна по величине весу, но имеет противоположный знак ): . Если движение происходит вверх P=m(g+a), вниз: P=m(g-a).

При свободном падении тела его вес равен нулю, т.е. оно находится в состоянии невесомости.

Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией. Упругая (квазиупругая) сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия: .

Силы трения являются одним из проявлений контактного взаимодействия тел, в частности сила трения скольжения возникает при скольжении одного тела по поверхности другого: и направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.

Упругие силы и силы трения определяются характером взаимодействия между молекулами вещества, которое имеет электромагнитное происхождение, следовательно они по своей природе имеют электромагнитные происхождения. Гравитационные и электромагнитные силы являются фундаментальными – их нельзя свести к другим, более простым силам. Упругие силы и силы трения не являются фундаментальными. Фундаментальные взаимодействия отличаются простотой и точностью законов.

Силы трения.

Трение является одним из проявлений контактного взаимодействия тел. Трение различают двух видов: внешнее и внутреннее.

Силы внешнего трения возникают на поверхности контакта двух тел. Внутреннее трение – это тангенциальное взаимодействие между слоями одного и того же тела. Если сила трения возникает при движении твердого тела в жидкой или газообразной среде, то ее относят к силам внутреннего трения.

Трение между поверхностями твердых тел при отсутствии какой-либо прослойки или смазки называется сухим. Трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды называется вязким или жидким.

Рассмотрим сухое трение. Различают три его вида: трение покоя, трение скольжения и трение качения.

а) Сила трения покоя – это сила, действующая между соприкасающимися телами, находящимися в состоянии покоя, равная по величине и противоположно направленная силе, понуждающей тело к движению.

До возникновения скольжения сила трения покоя может иметь любое направление и принимать любое значение от нуля до некоторого максимального, при котором возникает скольжение: .

Силу трения покоя, равную по модулю внешней силе, при которой начинается скольжение данного тела по поверхности другого, называют максимальной силой трения покоя.

Французские физики Г.Амонтон и Ш.Кулон установили, что: максимальная сила трения покоя пропорциональна силе реакции опоры (нормального давления) и не зависит от площади соприкосновения трущихся тел

где μ – коэффициент трения покоя, зависит от физической природы соприкасающихся тел и обработки их поверхностей,

б) Трение скольжения. Если к телу приложить внешнюю силу, превышающую , то тело начинает скользить. Сила трения продолжает существовать и называется силой трения скольжения.

Силы трения скольжения действуют вдоль поверхности контакта двух тел. Они приложены к обеим трущимся поверхностям в соответствии с третьим законом Ньютона. Модуль силы трения скольжения зависит от материала тел, состояния поверхностей и от относительной скорости движения тел (см. рис.4). Уменьшение силы трения скольжения при малых скоростях объясняется тем, что при движении тела, имеющиеся на его поверхности микроскопические выступы не успевают так глубоко западать в углубления поверхности другого тела, как при покое. Деформируются только «верхушки» выступов. Увеличение силы трения скольжения при больших скоростях связано с разрушением выступов и их размельчением. У грубо обработанной поверхности основную роль в возникновении сил трения покоя и скольжения играют зацепления неровностей, а при тщательной обработке – молекулярное или атомное сцепление. При специальной обработке поверхностей сила трения скольжения может практически не зависеть от скорости.

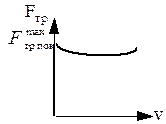
Рис.4

Силы трения скольжения также зависят от нормального давления на поверхность соприкосновения. При постоянной скорости движения:

Коэффициент трения скольжения μ_ск зависит от материала тел, состояния поверхностей и от относительной скорости движения тел. В первом приближении можно считать μ_ск равным коэффициенту трения покоя μ (μ_ск =μ). Для определения μ положим тело на наклонную плоскость и начнем увеличивать угол наклона α. Из (1) μ=F/N. При определенном значении α тело начинает движение вниз.

Тело приходит в движение, когда (рис.5) F=F_тр и F=mgsinα; N=mgcosα, тогда:

Таким образом, коэффициент трения равен тангенсу угла α₀, при котором начинается скольжение тела по наклонной плоскости.

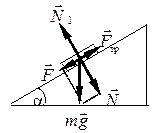
Рис.5

в) Трение качения. При качении тела по поверхности другого возникает особая сила – сила трения качения, которая препятствует качению тела. Сила терния качения при тех же материалах соприкасаемых тел всегда меньше силы терния скольжения. Этим пользуются на практике, заменяя подшипники скольжения шариковыми или роликовыми подшипниками. Кулон опытным путем установил для катящегося цилиндра радиуса R:

где μ_К – коэффициент трения качения, величина которого уменьшается с увеличением твердости материала и шероховатости его поверхности.

Для катящегося обода

На тело, движущееся в вязкой (жидкой или газообразной) среде, действует сила жидкого трения, тормозящая его движение.

Сила жидкого трения вместе со скоростью обращается в нуль. При небольших скоростях она растет пропорционально скорости:

Коэффициент k₁ зависит от формы и размеров тела, характера его поверхности, а также от свойства среды, называемого вязкостью.

При увеличении скорости линейная зависимость постепенно переходит в квадратичную:

k₂ также зависит от формы тела, от площади лобового сопротивления, от вязкости жидкости (ею пренебрегают).

Границы области, в которой происходит переход от закона (2) к закону (3), зависят от тех же факторов, от которых зависит коэффициент k₁.

Задачи динамики для свободной и несвободной материальной точки.

Для свободной материальной точки задачами динамики являются следующие:

1) зная закон движения точки, определить действующую на нее силу (первая задача динамики);

2) зная действующие на точку силы, определить закон движения точки (вторая или основная задача динамики).

Решаются обе эти задачи с помощью уравнений, выражающих основной закон динамики, так как эти уравнения связывают ускорение т.е. величину, характеризующую движение точки, и действующие на нее силы.

В технике часто приходится сталкиваться с изучением несвободного движения точки, т.е. со случаями, когда точка, благодаря наложенным на нее связям, вынуждена двигаться по заданной неподвижной поверхности или кривой.

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, которое называется уравнением связи.

f(x,y,z)=0

Если точка вынуждена двигаться по некоторой линии, то уравнениями связи являются уравнения этой лини.

.

Таким образом, движение несвободной материальной точки зависит не только от приложенных к ней активных сил и начальных условий, но так же от имеющихся связей. При этом значения начальных параметров должны удовлетворять уравнениям связей.

Связи бывают двухсторонние или удерживающие и односторонние или неудерживающие.

Связь называется двухсторонней если, накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве на которых должна находится точка.

Пример. Материальная точка подвешена на стержне длины l (рис.6).

Уравнение связи имеет вид:

x²+y²+z²=l²

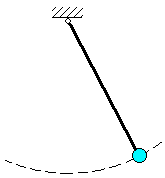
Рис.6

Связь называется односторонней если, накладываемые ею на координаты точки ограничения выражаются в форме неравенств. Односторонняя связь препятствует перемещению точки лишь в одном направлении и допускает ее перемещение в других направлениях.

Пример. Материальная точка подвешена на нити длины l (рис.7).

Уравнение связи имеет вид:

x²+y²+z²l²

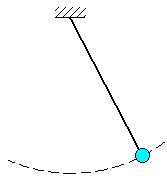
Рис.7

В случаях несвободного движения точки, как и в статике, будем при решении задач исходить из аксиомы связей (принцип освобождаемости от связей), согласно которой всякую несвободную материальную точку можно рассматривать как свободную, отбросив связь и заменив ее действие реакцией этой связи . Тогда основной закон динамики для несвободного движения точки примет вид:

,

где -действующие на точку активные силы.

Пусть на точку действует несколько сил. Составим для неё основное уравнение динамики: . Перенесём все члены в одну сторону уравнения и запишем так: или .

Это уравнение напоминает условие равновесия сходящихся сил. Поэтому можно сделать вывод, что, если к движущейся материальной точке приложить её силу инерции, то точка будет находиться в равновесии. (Вспомним, что на самом деле сила инерции не приложена к материальной точке и точка не находится в равновесии.) Отсюда следует метод решения таких задач, который называется методом кинетостатики:

Если к силам, действующим на точку, добавить ее силу инерции, то задачу можно решать методами статики, составлением уравнений равновесия.

Первая задача динамики для несвободного движения будет обычно сводиться к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи.

Методические указания по решению задач.

Решать задачи с применением законов динамики целесообразно следующим образом.

1) Выбрать систему отсчета - инерциальную или неинерциальную.

2) Установить, каким моделям объектов и движений соответствует физическая ситуация, описанная в условии задачи. Сделать рисунок.

3) Назвать все силы, действующие на каждое тело, указывая их происхождение. Изобразить силы на рисунке. Записать законы сил.

4) Записать законы динамики в векторной форме.

5) Выбрать и изобразить на рисунке оси координат. Ось х удобно направить по вектору ускорения. Можно для всех тел указать общую систему координат, иногда удобно каждому телу сопоставить свою систему.

6) Записать систему динамических уравнений в проекциях на оси координат.

7) Установить уравнения кинематической связи.

8) Проверить, является ли система уравнений полной, решить ее в общем виде.

9) Проанализировать полученный результат.

Примечание: при решении некоторых задач выполняются не все пункты алгоритма.

Пример 1. При движении автомобиля с постоянным ускорением , маятник (материальная точка подвешенная на нити) отклоняется от вертикали на угол (рис.8). Определим с каким ускорением движется автомобиль и натяжение нити.

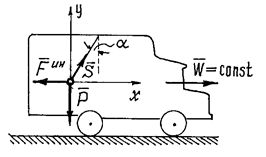
Рис.8

Решение. Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.

На точку действуют силы: вес и натяжение нити , реакция нити. Приложим к точке ее силу инерции , направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

;

.

Рис. 13.1.

Из второго уравнения следует

Из первого и .

Пример 2. Лифт весом Р (рис.9) начинает подниматься с ускорением a. Определить натяжение троса.

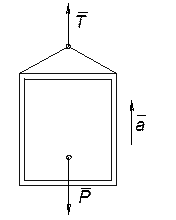
Рис. 9

Решение. Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение в проекции на вертикаль, получаем:

Отсюда находим:

Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:

Пример 3. Тело массой 300 кг лежит на полу кабины грузового подъемника, поднимающегося вверх (рис.10). Дано: m=300 кг, а=3 м/с² – ускорение кабины.

Определить силу давления тела на пол кабины Р.

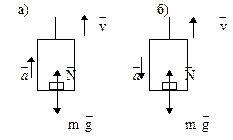
Рис.10

Решение. Основной закон динамики для тела запишется в виде:

где - сила реакции опоры.

Рассмотрим два случая:

а) ускорение направлено вверх: ma=N₁–mg,

отсюда N₁=ma+mg.

По третьему закону Ньютона Р₁=N₁ , Р₁= ma+ mg, Р₁=3,84 кН.

б) ускорение направлено вниз: -ma=N₂ - mg,

следовательно N₁=mg–ma, т.е. Р₂=mg- ma, Р₂=2,04 кН.

Пример 4. К нити подвешен груз (рис.11) массой m=1 кг. Найти силу натяжения нити Т, если 1) нить с грузом покоится; 2) двигается вниз с ускорением a= 5 м/с²; 3) двигается вверх с ускорением a= 5 м/с².

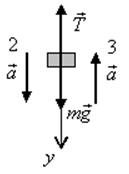
Рис.11

Решение. На тело действуют две силы: сила тяжести и сила натяжения . Уравнение движения тела (второй закон Ньютона) в данном случае имеет вид:

Выберем направление оси y вниз и спроецируем на нее векторы сил и ускорения:

1) =0 ⇒ 0=mg-T ⇒ T=mg=1∙9,8=9,8 Н.

2) направлено вниз ⇒ ma=mg-T ⇒ T=m∙(g-a)=1∙(9,8-5)=4,8 Н.

3) направлено вверх ⇒ ma=mg-T ⇒ T=m∙(g+a)=1∙(9,8+5)=14,8 Н.

Пример 5. Груз массой 50 кг перемещается по горизонтальной плоскости под действием силы F=300 Н, направленной под углом α=30° к горизонтали (рис.12). Коэффициент трения груза о плоскость μ=0,1. Определить ускорение, с которым движется груз.

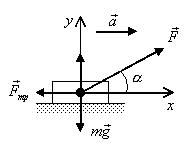
Рис.12

Решение. Уравнение движения тела

Выберем направления осей х и y и спроецируем на них силы и ускорение:

Поскольку F_тр=μN, а из второго уравнения N=mg-Fsinα, то F_тр=μ(mg-Fsinα). Тогда из первого уравнения ускорение

Пример 6. Санки массой m тянут по горизонтальной поверхности с силой F, направленной под углом α к горизонту (рис.12.1). Коэффициент трения между санками и горизонтальной поверхностью равен μ. Определить ускорение санок.

Рис.12.1

Решение.

1. Движение рассматривается относительно Земли, которую считаем инерциальной системой отсчета.

2. В задаче рассматривается поступательное движение твердого тела.

3. На санки действует Земля с силой тяжести mg, веревка с силой F и горизонтальная поверхность с силами нормального давления N и силой трения скольжения F_тр, модуль которой равен

4. Запишем второй закон Ньютона в векторной форме:

5. Выберем оси координат таким образом, чтобы ось х была направлена по вектору ускорения.

6. Спроектируем векторное уравнение на оси координат:

8. В эти три уравнения входят три неизвестных: F_тр, N и а, то есть система уравнений является полной. Разрешим эту систему. Из (3) находим N=mg-Fsinα, из (1) F_тр=μ(mg-Fsinα). Подставляя в (2), получаем

9. Обратим внимание, что сила нормального давления N по величине меньше силы тяжести mg, т.к. вертикальной составляющей силы F санки приподнимаются, а следовательно уменьшается их взаимодействие с горизонтальной поверхностью.

Пример 7. Тело лежит на наклонной плоскости, образующей с горизонтом угол α=5° (рис.13). При каком предельном коэффициенте трения μ_пр тело начнет скользить по наклонной плоскости? С каким ускорением будет двигаться тело, если коэффициент трения μ=0,02? Какое время t понадобиться для прохождения при этих условиях пути s=10 м. Какую скорость тело будет иметь в конце наклонной плоскости?

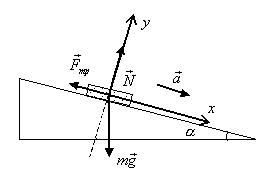
Рис.13

Решение. Запишем II закон Ньютона для данного тела

Выбрав оси х и y, спроецируем на них силы и ускорение:

1) Для первого случая, когда μ=μ_пр и a=0, имеем

откуда

2) Во втором случае μ<μ_пр, поэтому тело будет скользить по наклонной плоскости с ускорением

Поскольку тело движется равноускоренно из состояния покоя, то время прохождения им расстояния s=10 м и скорости в конце этого пути можно найти из уравнений кинематики

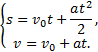
Положив v₀=0. Получим:

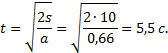
Пример 8. Брусок массы m втаскивают за нить вверх по наклонной плоскости, составляющей угол a с горизонтом (рис.13.1). Сила натяжения нити равна F, угол между нитью и наклонной плоскостью β, коэффициент трения скольжения между бруском и плоскостью равен μ. Найти ускорение бруска.

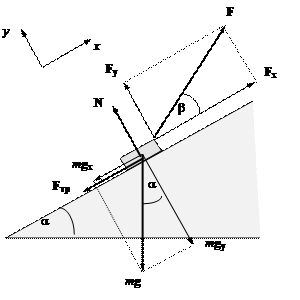
Рис.13.1

Решение.

1) В задаче описано поступательное движение бруска относительно Земли, которую считаем инерциальной системой отсчета.

2) На брусок действуют:

- Земля с силой тяжести mg;

- нить с силой F;

- наклонная плоскость с силами нормального давления N и трения F_тр, причем,

3) По второму закону Ньютона

4) Направим ось х вверх вдоль наклонной плоскости (по ускорению в соответствии с условием задачи).

5) Спроектируем векторное уравнение на оси координат:

6) Получена система трех уравнений с тремя неизвестными. Из (3) находим величину силы нормального давления , из (1) - величину силы трения . Подставляя полученное выражение в (2), находим искомое ускорение

Пример 9. Под действием силы F = 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути S от времени t дается уравнением S=A-Bt+Ct², где С = 1 м/с². Найти массу m тела.

Решение. 1) Известно, что зависимость пути от времени выражается формулой:

Отсюда имеем:

2) По условию: C=1 м/с² следовательно: a=2C=2 м/с²

3) Из второго закона Ньютона: F=ma отсюда: m=F/a=10/2=5 кг.

Пример 10. Точка массы т движется в плоскости Оху согласно уравнениям х=аsinωt; у=bcosωt (рис.13.2). Найти силу, действующую на точку.

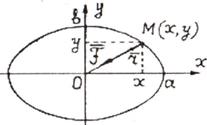
Рис.13.2

Решение. Найдем траекторию точки. Исключив время t из уравнений ее движения. Получим

Траекторией точки М является эллипс с полуосями а и в.

При t = 0: х₀ = 0 и у= b. Точка движется по эллипсу по часовой стрелке.

Проекции приложенной к точке силы , а оси координат:

Проекции радиус-вектора точки М на оси координат и длина этого вектора

Далее получаем

Сила направлена к точке О и ее величина пропорциональна расстоянию от начала координат до точки приложения этой силы.

Пример 11. Груз М массы m = 0,102 кг, подвешенный на нити длиной ОМ = 1 = 0,3 м в точке О, представляет собой конический маятник, т.е. описывает окружность в горизонтальной плоскости, причем нить составляет с вертикалью угол α = 60° (рис.13.3).

Определить скорость v груза и натяжение T нити.

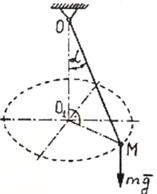
Рис.13.3

Решение. Будем считать груз материальной точкой. Приложим к точке М силу тяжести mg и натяжение нити Т.

Построим подвижную естественную систему координат M𝜏nb.

Суммы проекций приложенных к точке сил на указанные оси

Составим дифференциальные уравнения движения точки в подвижной естественной системе координат

Из системы уравнений находим

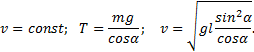
С учетом исходных данных получаем

Пример 12. Ледяная горка составляет с горизонтом угол α (рис.14). По ней пускают вверх камень, который после подъема съезжает вниз. Дано: t₂/t₁=n.

Чему равен коэффициент трения μ, если время спуска в n раз больше времени подъема.

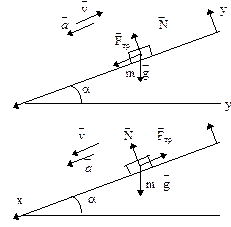
Рис.14

Решение. Уравнение движения камня

При движении вверх - движение равнозамедленное. В проекциях на оси ОХ и OY: ma₁=F_тр+mg∙sinα; N-mg∙cosα=0,

откуда N= mg∙cosα. Тогда сила трения F_тр =μN=μmg∙cosα, и окончательно уравнение движения

При движении вниз:

Проведя аналогичные преобразования, получим уравнение движения в этом случае:

Из (1) и (2):

При движении вверх камень проходит путь ; скорость в конце подъема v=0, следовательно v_o= a₁t₁, тогда

При движении вниз камень проходит путь

Из (3) и (4) получим

Используя (1) и (2):

отсюда

Пример 13. На рис.14.1,а изображен качающийся маятник, на рисунке 14.1,б - конический маятник. Верно ли представлено соотношение сил mg и Т на рисунках 14.1,а и 14.1,б?

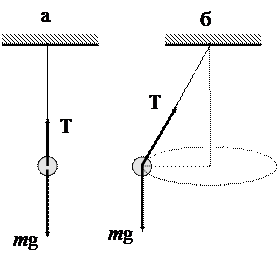
Рис.14.1

Решение. В обоих случаях материальная точка движется по окружности. Вектор полного ускорения складывается из нормального ускорения a_n, направленного к центру окружности, и тангенциального a_τ, направленного по касательной к окружности. По второму закону Ньютона ускорение определяется равнодействующей силой, то есть ma=mg+T. Направления равнодействующей силы и ускорения совпадают.

В случае 14.1,а равнодействующая сила ориентирована вертикально, поэтому a_τ =0 и полное ускорение равно нормальному ускорению, a = a_n. Оно направлено к центру окружности, то есть вверх. Поэтому сила натяжения нити по величине должна быть больше силы тяжести. Соотношения между силами представлены неверно.

В случае 14.1,б материальная точка движется по окружности с постоянной скоростью. Ускорение при таком движении направлено к центру окружности. Во втором законе Ньютона ma=mg+T силы являются сторонами параллелограмма, а ma - его диагональю. Произведя на рисунке сложение векторов, можно сделать вид, что соотношения между силами представлены правильно.

Пример 14. Для материальной точки, движущейся по окружности, дан график зависимости скорости от времени v(t) (рис.15). Указать направление результирующей силы, действующей на материальную точку в положении М.

Рис.15

Решение. Скорость направлена по касательной к траектории. Из графика видно, что в момент времени t_M величина скорости уменьшается, поэтому тангенциальное ускорение a_𝛕 противоположно вектору скорости. Нормальное ускорение a_n направлено к центру окружности.

Рис.15.1

Изобразим вектор полного ускорения a=a_n+a_τ (рис.15.1). Направление равнодействующей силы совпадает с вектором полного ускорения.

Пример 15. Два маленьких шарика, массы которых равны m₁ и m₂, привязаны к нити один за другим и вращаются в горизонтальной плоскости с угловой скоростью ω (рис.16). Расстояния от шариков до оси вращения l₁ и l₂. Определить силы натяжения нитей.

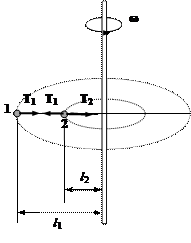
Рис.16

Решение. Поскольку силой тяжести в данной задаче можно пренебречь, (по условию шарики вращаются в горизонтальной плоскости), будем считать, что на шарики действуют только нити: на шарик 1 одна нить с силой T₁, на шарик 2 - две нити с силами T₁ и T₂.

Запишем второй закон Ньютона сразу в проекциях на рaдиальное направление.

Для шарика 1: m₁a₁=T₁, (1)

для шарика 2: m₂a₂=T₂-T₁. (2)

Существенным условием данной задачи является равномерное движение материальных точек по окружности. При таком движении линейные скорости шариков не меняются по величине, а следовательно, тангенциальное ускорение равно нулю. Вектор полного ускорения направлен к центру окружности, а его величина связана с угловой скоростью ω и радиусом окружности r соотношением

Таким образом, величина ускорения каждого шарика соответственно равна и . С учетом этих соотношений уравнения динамики (1) и (2) примут вид

Отсюда получаем выражения для искомых сил:

Пример 16. Автомобиль массой m = 5 тонн проходит по выпуклому мосту со скоростью v=36 км/ч (рис.17). С какой силой F он давит на середину моста, если радиус кривизны моста R=100 м? Какова будет сила давления, если мост будет вогнутый с тем же радиусом кривизны?

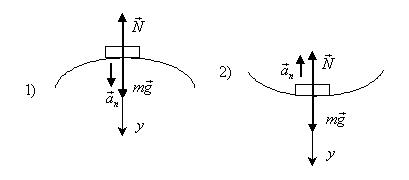
Рис.17

Решение. На основании II закона Ньютона запишем уравнение движения автомобиля:

Выберем направление оси y и спроецируем на нее силы и ускорение. Обратим внимание на то, что поскольку движение автомобиля равномерное криволинейное, то ускорение

По III закону Ньютона сила, с которой автомобиль давит на мост, равна по модулю силе, с которой мост давит на автомобиль, т.е. силе нормальной реакции опоры N.

1) Уравнение движения в проекциях для первого случая имеет вид

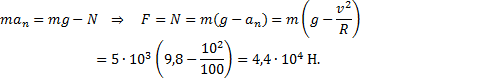
2) Для второго случая

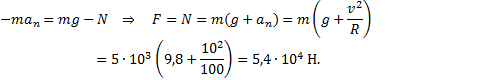
Пример 17. На сколько должен быть поднят наружный рельс над внутренним (рис.18) на закруглении железнодорожного пути радиусом 300 м, если ширина колеи 1524 мм? Скорость, при которой сила давления на рельсы перпендикулярна им, принять равной 54 км/ч.

Дано: R=300 м, l=1,524 м, v=15 м/с.

Найти: h - ?

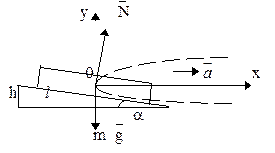
Рис.18

Решение. Поезд должен двигаться по окружности радиуса R со скоростью v, т.е. с ускорением a=v²/R, направленным горизонтально. Это ускорение вызывает равнодействующая сил . Поэтому наружный рельс должен быть приподнят на некоторую высоту h.

Второй закон Ньютона

в проекциях на оси ОХ и OY:

ma = N∙sinα,

N∙cosα - mg = 0.

Откуда

Так как угол α мал, то sinα≈tgα.

Из рис.18

Следовательно,

h=0,12 м.

Пример 18. На экваторе некоторой планеты тело весит вдвое меньше, чем на полюсе P=Р_п/2 (рис.19). Плотность вещества этой планеты ρ=3∙10³ кг/м³. Определить период вращения планеты T вокруг своей оси.

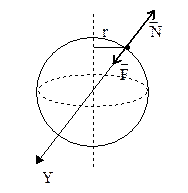
Рис.19

Решение. На тело, находящееся на поверхности планеты, действуют: - сила тяготения со стороны планеты, – сила нормальной реакции планеты (рис.19).

По определению, , где М - масса планеты, m - масса тела, R-радиус планеты.

Масса планеты: , а

По второму закону Ньютона:

в скалярной форме относительно оси Y:

F – N = ma_n, (2)

или

Рассмотрим два частных случая движения тела.

1. Тело находится на полюсе, т.е. r=0, тогда линейная скорость тела

Следовательно, уравнение (3) примет вид , откуда

N_п - сила нормальной реакции на полюсе.

2. Тело находится на экваторе. В этом случае r=R и v=2πr/T. Тогда уравнение (3) примет вид: , откуда

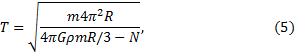
где N - сила нормальной реакции поверхности на экваторе.

По условию задачи, Р_э=Р_п/2.

Поскольку Р=N, то N=N_п/2, или с учетом (4)

Подставим формулу (6) в (5):

Дифференциальные уравнения движения точки

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

1) Определение движения точки координатным способом.

Рассмотрим свободную материальную точку, движущуюся под действием сил . Проведем неподвижные координатные оси Oxyz (рис.20). Проектируя обе части равенства на эти оси и учитывая, что и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:

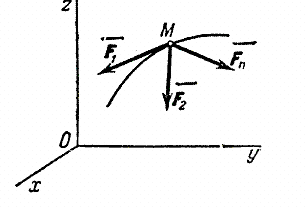
Рис.20

Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости . При этом в правую часть каждого из уравнений могут входить все эти переменные.

Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при t=0

Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.

Пример 19. Найти закон движения материальной точки массы m, движущейся вдоль оси х под действием постоянной по модулю силы F (рис. 20.1) при начальных условиях: при t=0.

Рис.20.1

Решение. Составим дифференциальное уравнение движения точки в проекции на ось х: . Интегрируя это уравнение, находим: . Постоянная C₁ определяется из начального условия для скорости и равна . Окончательно

Далее, учитывая, что v = dx/dt, приходим к дифференциальному уравнению: , интегрируя которое получаем

Постоянную C₂ определяем из начального условия для координаты точки. Она равна . Следовательно, закон движения точки имеет вид

Пример 20. Груз веса Р (рис.20.2) начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F = kt. Найти закон движения груза.

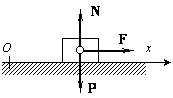
Рис.20.2

Решение. Выберем начало отсчета системы координат О в начальном положении груза и направим ось х в сторону движения (рис. 20.2). Тогда начальные условия имеют вид: x(t = 0) = 0, v(t = 0) = 0. На груз действуют силы F, P и сила реакции плоскости N. Проекции этих сил на ось х имеют значения F_x = F = kt, Р_x = 0, N_x = 0, поэтому соответствующее уравнение движения можно записать так: . Разделяя переменные в этом дифференциальном уравнении и затем интегрируя, получим: v = gkt²/2P + C₁. Подставляя начальные данные (v(0) = 0), находим, что C₁ = 0, и получаем закон изменения скорости .

Последнее выражение, в свою очередь, является дифференциальным уравнением, интегрируя которое найдем закон движения материальной точки: . Входящую сюда постоянную определяем из второго начального условия х(0) = 0. Легко убедиться, что C₂=0. Окончательно

Пример 21. На груз, находящийся в покое на горизонтальной гладкой плоскости (см. рис. 20.2) на расстоянии a от начала координат, начинает действовать в положительном направлении оси x сила F = k²(P/g)x, где Р – вес груза. Найти закон движения груза.

Решение. Уравнение движения рассматриваемого груза (материальной точки) в проекции на ось х

Начальные условия уравнения (1) имеют вид: x(t = 0) = a, v(t = 0) = 0.

Входящую в уравнение (1) производную по времени от скорости представим так

Подставляя это выражение в уравнение (1) и сокращая на (P/g), получим

Разделяя переменные в последнем уравнении, находим, что . Интегрируя последнее, имеем: . Используя начальные условия , получаем , и, следовательно,

Поскольку сила действует на груз в положительном направлении оси х, то ясно, что в том же направлении он должен и двигаться. Поэтому в решении (2) следует выбрать знак "плюс". Заменяя дальше во втором выражении (2) v на dx/dt, получаем дифференциальное уравнение для определения закона движения груза. Откуда, разделяя переменные, имеем

Интегрируя последнее, находим: arch x/a=kt+C₂. После нахождения постоянной C₂ окончательно получаем

arch x/a=kt или .

Пример 22. Шар M массы m (рис.20.3) падает без начальной скорости под действием силы тяжести. При падении шар испытывает сопротивление , где – постоянный коэффициент сопротивления. Найти закон движения шара.

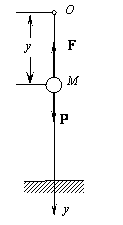
Рис.20.3

Решение. Введем систему координат с началом в точке местоположения шара при t = 0, направив ось у вертикально вниз (рис. 20.3). Дифференциальное уравнение движения шара в проекции на ось у имеет тогда вид

. (1)

Начальные условия для шара записываются так: y(t = 0) = 0, v(t = 0) = 0.

Разделяя переменные в уравнении (1)

и интегрируя, находим: , где . Или после нахождения постоянной

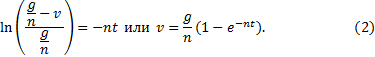
Отсюда следует, что предельная скорость, т.е. скорость при , равна .

Чтобы найти закон движения, заменим в уравнении (2) v на dy/dt. Тогда, интегрируя полученное уравнение с учетом начального условия, окончательно находим

Пример 23. Изучим движение тела, брошенного с начальной скоростью v₀ под углом к горизонту, рассматривая его как материальную точку массы т (рис.21). При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.

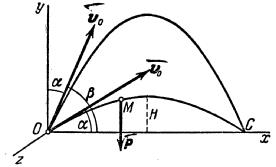
Рис.21

Решение. Поместим начало координат О в начальном положении точки. Направим ось Oy вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор v₀, а ось Oz проведём перпендикулярно первым двум осям (рис.21). Тогда угол между вектором v₀ и осью Ox будет равен .

Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести , проекции которой на оси координат равны: P_x=0, P_y=-P=-mg, P_z=0.

Подставляя эти величины в дифференциальные уравнения и замечая, что /dt = и т.д. мы после сокращения на m получим:

Умножая обе части этих уравнений на dt и интегрируя, находим:

V_x=C₁, V_y=-dt+C₂, V_z=C₃

Начальные условия в нашей задаче имеют вид:

при t=0:

Удовлетворяя начальным условиям, будем иметь:

Подставляя эти значения С₁, С₂ и С₃ в найденное выше решение и заменяя v_x, v_y, v_z на придём к уравнениям:

Интегрируя эти уравнения, получим:

Подстановка начальных данных даёт С₄=С₅=С₆=0, и мы окончательно находим уравнения движения точки М в виде:

Из последнего уравнения следует, что движение происходит в плоскости Оxy.

Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.

1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:

Это - уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).

2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:

получаем

Первое решение дает точку О, второе точку С. Следовательно, Х=Х₂ и окончательно

Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле , для которого , т.е. если угол . Следовательно, при данной начальной скорости в одну и ту же точку С можно попасть двумя траекториями: настильной () и навесной ().

При заданной начальной скорости V₀ наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда , т.е. при угле .

3. Высота траектории. Если положить в уравнении (2)

, то найдется высота траектории Н:

. (4)

4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством . Заменяя здесь Х его значением, получим

При угле наибольшей дальности все найденные величины равны:

Полученные результаты практически вполне приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивление воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.

Пример 24. Из пушки, установленной на высоте h, произвели выстрел под углом к горизонту (рис. 22). Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.

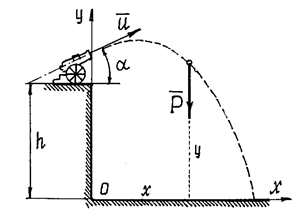
Рис.22

Решение. Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.

а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.

б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.22).

в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).

В этом примере – это только сила , вес ядра. Сопротивление воздуха учитывать не будем.

г) Составить дифференциальные уравнения по формулам: . Отсюда получим два уравнения: и .

д) Решить дифференциальные уравнения.

Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.

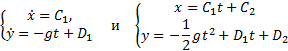
Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, ) в эти четыре уравнения: .

Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде

Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.

Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.

Пример 25. Материальная точка массой m движется прямолинейно (рис.22.1) под действием силы F=F₀cos𝜔t (F₀ и ω — постоянные величины). Пренебрегая весом, определить скорость и положение точки в момент времени t₁=π/2ω, если она в начальный момент находилась в начале координат и ее скорость была равна v₀.

Рис.22.1

Решение. Точка движется прямолинейно, поэтому достаточно одной оси координат. Направим ось Ох вдоль траектории точки. Изобразим точку в промежуточном положении на ее траектории. Приложим к точке силу F (другие силы отсутствуют).

Составим уравнение движения точки

Скорость точки

Подставим начальные условия t = 0; v = v₀. Так как sin0 = 0, получим С₁ = v₀.

Закон движения точки:

Подставим начальные условия t = 0; х = 0. Ввиду того, что cos0 = 1, получим С₂ =F₀/(mω²).

Находим для момента времени t₁=𝜋/(2𝜔)

Пример 26. Груз весом Р движется вниз по шероховатой наклонной плоскости, составляющей угол α=30° с горизонтом. Коэффициент трения скольжения груза о плоскость f=0,16. В начальный момент груз находился в положении М_о на расстоянии a=9 м от начала координат и имел скорость v₀=30 м/с. Определить уравнение движения груза в заданной системе координат (рис. 22.2).

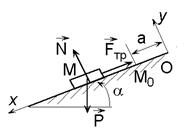
Рис.22.2

Решение. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (шероховатой наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения F_тр. Тогда тело будет двигаться под действием системы трех сил (Р, N, F_тр).

Примем тело за материальную точку. Проектируя основное уравнение динамики точки

на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:

Здесь m – масса точки; – проекции ускорения точки на соответствующие оси.

Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю, следовательно, уравнение (2) примет вид

Сила трения по закону Кулона равна . С учетом этого выражения дифференциальное уравнение (1) примет следующий вид:

После замены P=mg, где g – ускорение свободного падения тела, и очевидных преобразований получим следующее дифференциальное уравнение второго порядка:

Для понижения порядка уравнения произведем замену получим дифференциальное уравнение первого порядка с разделяющимися переменными:

Разделив переменные, проинтегрируем дифференциальное уравнение с учетом начальных условий (при t=0, v_x=v₀):

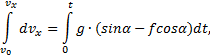
Произведем замену для понижения порядка уравнения и, разделив переменные, проинтегрируем дифференциальное уравнение второй раз с учетом начальных условий (при t=0 x=x₀=a):

Подставив в соотношение (4) значения заданных величин, получим окончательно следующее уравнение движения груза:

2) Определение движения точки естественным способом.

Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.

Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 23).

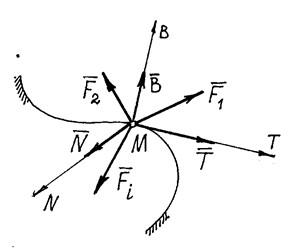
Рис.23

На точку М кроме заданных активных сил , действует реакция линии. Показываем составляющие реакции по естественным осям .

Составим основное уравнение динамики и спроектируем его на естественные оси

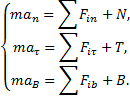
Так как , то получим дифференциальные уравнения движения, такие

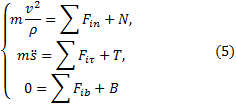
Здесь сила - сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:

Решив это уравнение, получим закон движения точки s=s(t), а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции и .

Рис. 13.5.

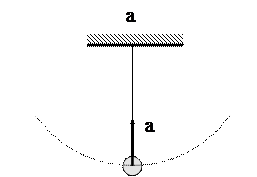
Пример 27. Лыжник спускается по цилиндрической поверхности радиуса r. Определим его движение, пренебрегая сопротивлениями движению (рис. 24).

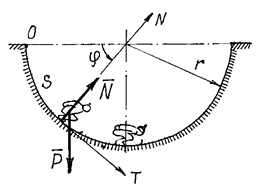
Рис.24

Решение. Схема решения задачи та же, что и при координатном способе (пример 15). Отличие лишь в выборе осей. Здесь оси N и Т движутся вместе с лыжником. Так как траектория – плоская линия, то ось В, направленную по бинормали, показывать не нужно (проекции на ось В действующих на лыжника сил будут равны нулю).

Дифференциальные уравнения по (5) получим такие

Первое уравнение получилось нелинейным: . Так как , то его можно переписать так: . Такое уравнение можно один раз проинтегрировать. Запишем . Тогда в дифференциальном уравнении переменные разделятся: . Интегрирование дает решение Так как при t = 0: и , то С₁= 0 и , а .

К сожалению, в элементарных функциях второй интеграл найти невозможно. Но и полученное решение позволяет сделать некоторые выводы. Можно найти скорость лыжника в любом положении как функцию угла . Так в нижнем положении, при . А из второго уравнения (6) при можно определить давление: . То есть давление на лыжника в нижнем положении равно его трехкратному весу.

Пример 28. Научно-исследовательская подводная лодка шарообразной формы и массы m = 1.5∙10⁵ кг начинает погружаться с выключенными двигателями, имея горизонтальную скорость v_х0 = 30 м/с и отрицательную плавучесть Р₁ = 0,01mg, где P₁=mg+Q – векторная сумма архимедовой выталкивающей силы Q и силы тяжести mg, действующих на лодку (рис. 24.1). Сила сопротивления воды R=- кг/с. Определить уравнения движения лодки и ее траекторию.

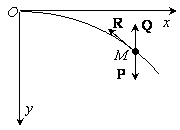
Рис.24.1

Решение. Начало координат выберем в начальном положении лодки, ось Ox направим горизонтально, а ось Oy – вертикально вниз (см. рис. 24.1). На лодку действуют три силы: P=mg – вес лодки, Q – архимедова выталкивающая сила, причем mg>Q, и сила сопротивления R. Лодку примем за материальную точку M. Тогда второй закон Ньютона запишется так: . В проекциях на оси Ox и Oy он будет иметь вид: . Перепишем эти уравнения в форме системы уравнений первого порядка

Интегрируя их методом разделения переменных, получаем

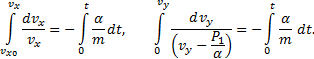
После интегрирования и подстановки численных значений параметров и начальных данных находим

Закон движения находим из решения дифференциальных уравнений

Он описывается соотношениями

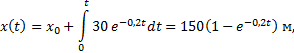
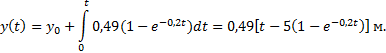
В заключение найдем траекторию y (x). Для этого из первого уравнения выразим время t через координату х

Подставляя это выражение во второе уравнение, находим

Пример 29. Точка, имеющая массу m, движется из состояния покоя по окружности радиуса R с постоянным касательным ускорением (рис.25). Определить действующую на точку силу в момент, когда она пройдет по траектории расстояние .

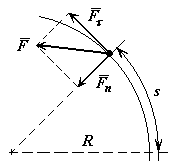
Рис.25

Решение. Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

;

Так как , то

;

,

; следовательно ;

следовательно

.

.

Пример 30. Груз массы m подвешен на нити длиной l. В начальный момент времени груз отклонили в сторону (нить натянута) и сообщили ему горизонтальную скорость, перпендикулярную нити (рис.25.1). Найти величину скорости груза и натяжение нити, если нить составляет с вертикалью постоянный угол α.

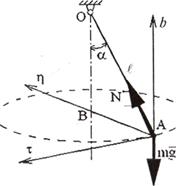
Рис.25.1

Решение. Будем считать груз материальной точкой. Приложим к грузу силу тяжести mg и натяжение нити N.

Как следует из условия задачи, при движении груза нить описывает коническую поверхность, траекторией груза является окружность с центром в точке В и радиусом АВ=lsinα. Если известна траектория точки, воспользуемся естественной системой координат (AτNb) и уравнениями движения в естественной форме

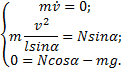
Из первой формулы следует, что скорость движения груза будет постоянной по величине, т.е. будет сохранить начальное значение. Из третьей формулы можем выразить натяжение нити

Подставив полученное выражение силы натяжения во вторую формулу, получим

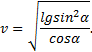
Относительное движение материальной точки

В предыдущем параграфе показано было как определяется движение точки относительно неподвижной системы отсчета, абсолютное движение. Нередко приходится исследовать движение материальной точки относительно системы, которая сама движется и довольно сложным образом.

Точка М (рис.26) под действием некоторых сил совершает сложное движение. Абсолютное определяется координатами x, y, z, относительное – координатами x₁, y₁, z₁.

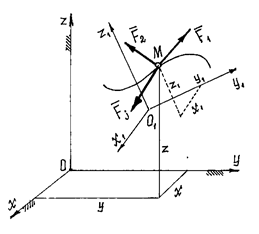
Рис.26

Составим основное уравнение динамики для точки , где абсолютное ускорение . Поэтому уравнение будет таким или .

Рис. 13.6.

Но - переносная сила инерции, - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так

Спроектировав это векторное равенство на подвижные оси x₁, y₁, z₁, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения

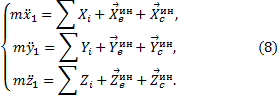
Сравнивая эти уравнения с дифференциальными уравнениями абсолютного движения, замечаем, что относительное движение материальной точки определяется такими же методами, что и абсолютное, надо лишь кроме обычных сил учесть переносную силу инерции и кориолисову силу инерции.

Если переносное движение поступательное, равномерное и прямолинейное, т.е. подвижная система инерциальная, то ускорение и . Значит и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).

Поэтому невозможно установить, наблюдая за движением точки, движется система поступательно, равномерно и прямолинейно или находится в покое. Этот вывод впервые был сделан Г.Галилеем и называется его именем – принцип относительности Галилея.

Физические величины и физические законы, не изменяющиеся при переходе от одной инерциальной системы отсчета к другой, называют инвариантными (не изменяющимися) к преобразованиям Галилея.

Пример 31. Вагон движется с постоянным ускорением . Определим траекторию движения предмета М, упавшего с полки высотой h, которую увидит наблюдатель, пассажир, сидящий в вагоне (рис.27).

Рис. 13.7.

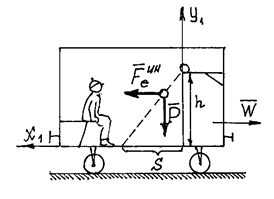
Рис.27

Решение. Порядок решения задачи тот же, что и при определении абсолютного движения. Только оси надо провести по вагону и учесть кроме веса предмета переносную силу инерции (кориолисова сила инерции – переносное движение поступательное).

Дифференциальные уравнения относительного движения получаются такими

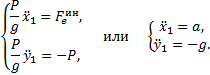
Решение этих уравнений

.

Используя начальные условия (при t = 0: x₁ = 0, y₁ = h, т.к. ), найдем постоянные интегрирования: C₁=C₂=D₁=0, D₂=h. Поэтому уравнения движения: Траекторию движения получим, исключив параметр t: Это уравнение прямой (рис. 27). Предмет М упадет на пол вагона на расстоянии от края полки (при ).

Если вагон будет двигаться равномерно (W = 0), то s = 0. Наблюдатель увидит траекторию – вертикальную прямую, такую же, как и при неподвижном вагоне.

Пример 32. Внутри трубки, вращающейся с постоянной угловой скоростью вокруг вертикальной оси, находится шарик М, привязанный нитью длиной а к оси вращения (рис. 28). Определим движение шарика в трубке после того, как нить оборвется. Сопротивление воздуха учитывать не будем.

Рис. 13.8.

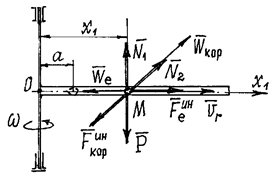
Рис.28

Решение. Траектория движения шарика в трубке – прямая. Поэтому для определения этого движения достаточно одной координаты х₁. Начало координат, точка О, - на оси вращения. В промежуточном положении на шарик действуют силы: вес , две составляющие реакции трубки . Добавляем переносную силу инерции кориолисову силу инерции и составляем дифференциальное уравнение движения: . Или, после подстановки значения силы инерции и преобразований: .

Решение такого дифференциального уравнения, как известно, имеет вид: и .

Так как при t = 0 x₁ = 0, , то С₁ +С₂ = а, С₁ – С₂ = 0.

Значит C₁=C₂=a/2 и уравнение движения станет таким

Относительная скорость . А т.к. , то

Можно теперь определить относительную скорость шарика в любом положении. Так шарик вылетит из трубки длиной l со скоростью

Влияние вращения Земли на равновесие и движение тел.

При решении большинства технических задач мы считаем систему отсчета, связанную с Землей, неподвижной (инерциальной). Тем самым мы не учитываем суточное вращение Земли и ее движение по орбите вокруг Солнца. Таким образом, считая систему отсчета, связанную с Землей, инерциальной, мы по существу пренебрегаем ее суточным вращением вместе с Землей по отношению к звездам. Это вращение происходит со скоростью: 1 оборот за 23 часа 56 минут 4 секунды, т. е. с угловой скоростью

Исследуем, как сказывается такое довольно медленное вращение на равновесии и движении тел.

1. Относительный покой на поверхности Земли. Сила тяжести. Рассмотрим материальную точку, лежащую на неподвижной относительно Земли гладкой «горизонтальной» плоскости (рис.29). Условие ее равновесия по отношению к Земле состоит в том, что , где - сила притяжения Земли, - реакция плоскости, -переносная сила инерции. Так как , то сила имеет только нормальную составляющую, направленную перпендикулярно к оси вращения Земли. Сложим силы и введем обозначение

.

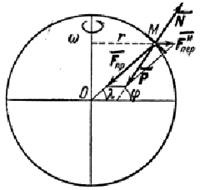
Рис.29

Тогда на точку М будут действовать две силы и , уравновешивающие друг друга. Сила и представляет собою ту силу, которую мы называем силой тяжести.

Направление силы будет направлением вертикали в данном пункте поверхности, а плоскость, перпендикулярная к и будет горизонтальной плоскостью. По модулю (r - расстояние точки М от земной оси) и величина малая по сравнению с , так как величина очень мала. Направление силы мало отличается от направления _.

При взвешивании тел мы определяем силу , т.к. именно с такой силой тело давит на тело весов. То есть, вводя в уравнения равновесия силу тяжести , мы вводим в них и силу , т.е. фактически учитываем влияние вращения Земли.

Поэтому при составлении уравнений равновесия тел по отношению к Земле никаких поправок на вращение Земли вводить не надо. В этом смысле равновесие по отношению к Земле можно считать абсолютным.

а) Движение по земной поверхности. При движении точки по меридиану в северном полушарии с севера на юг кориолисово ускорение направлено на восток, а сила - на запад. При движении с юга на север сила будет, очевидно, направлена на восток. В обоих случаях, как мы видим, эта сила будет отклонять точку вправо от направления ее движения. Если точка движется по параллели на восток, то ускорение будет направлено вдоль радиуса МС параллели (рис.30), а сила в противоположную сторону. Вертикальная составляющая этой силы (вдоль ОМ) будет несколько изменять вес тела, а горизонтальная составляющая будет направлена к югу и будет отклонять точку тоже вправо от направления движения. Аналогичный результат получим при движении по параллели на запад.

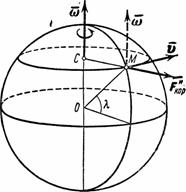
Рис.30

Отсюда заключаем, что в северном полушарии тело, движущееся вдоль земной поверхности по любому направлению будет вследствие вращения Земли отклоняться вправо от направления движения. В южном полушарии отклонение будет происходить влево.

Этим обстоятельством объясняется то, что реки, текущие в северном полушарии, подмывают правый берег (закон Бэра). В этом же причина отклонений ветров постоянного направления (пассаты) и морских течений.

Общие теоремы динамики точки

Для решения многих задач динамики, особенно в динамике системы, вместо метода интегрирования дифференциальных уравнений движения оказывается более удобным пользоваться так называемыми общими теоремами, являющимися следствиями основного закона динамики.

Значение общих теорем состоит в том, что они устанавливают наглядные зависимости между основными динамическими характеристиками движения материальных тел и открывают тем самым новые возможности исследования движений механических систем, широко применяемые в инженерной практике. Кроме того, общие теоремы позволяют изучать отдельные, практически важные стороны данного явления, не изучая явление в целом. Наконец, применение общих теорем избавляет от необходимости проделывать для каждой задачи те операции интегрирования, которые раз и навсегда производятся при выводе этих теорем; тем самым упрощается процесс решения. Сейчас мы рассмотрим, как выглядят эти теоремы для одной материальной точки.

Количество движения (импульс) точки

Основными динамическими характеристиками движения точки являются количество движения и кинетическая энергия.

Количеством движения точки называется векторная величина равная произведению массы точки на вектор ее скорости. Направлен вектор так же, как и скорость точки, т. е. по касательной к ее траектории.

Кинетической энергией (или живой силой) точки называется скалярная величина 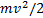, равная половине произведения массы точки на квадрат ее скорости.

Необходимость введения двух динамических характеристик объясняется тем, что одной характеристикой нельзя охватить все особенности движения точки.

Например, зная количество движения автомобиля (т.е. величину Q=mv) а не величины m и v в отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормозной путь, но по этим данным нельзя найти время торможения.

Импульс силы

Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т. е. об импульсе за бесконечно малый промежуток времени dt. Элементарным импульсом силы называется векторная величина , равная произведению вектора силы на элементарный промежуток времени dt.

.

Направлен элементарный импульс по линии действия силы.

Импульс любой силы за конечный промежуток времени t₁ вычисляется как интегральная сумма соответствующих элементарных импульсов:

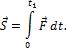
Следовательно, импульс силы за любой промежуток времени, равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до .

В частном случае, если сила и по модулю, и по направлению постоянна (), будем иметь . Причем, в этом случае и модуль . В общем случае модуль импульса может быть вычислен через его проекции.

Проекции импульса силы на прямоугольные декартовы оси координат равны:

.

Единицей измерения импульса в СИ является – 1 .

Пример 33. Стальной шарик массой m = 10 г, летящий со скоростью v=100 м/с по нормали к стенке, ударяется о нее и упруго отскакивает без потери скорости (рис.31). Найти импульс, полученный стенкой за время удара.

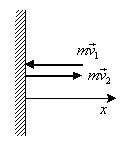
Рис.31

Решение. Из II закона Ньютона

Величина называется импульсом силы. Видно, что по модулю импульс силы равен

т.е. изменению импульса шарика.

Выберем ось х и спроецируем импульсы шарика:

Поскольку по условию задачи v₁=v₂=v, то F∆t=2mv=2∙10^-2∙10²=2 кг∙м/с.

Теорема об изменении количества движения точки

Так как масса точки постоянна, а ее ускорение то уравнение, выражающее основной закон динамики, можно представить в виде

Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме действующих на точку сил.

Проинтегрируем это уравнение. Пусть точка массы m, движущаяся под действием силы (рис.32), имеет в момент t=0 скорость , а в момент t₁- скорость .

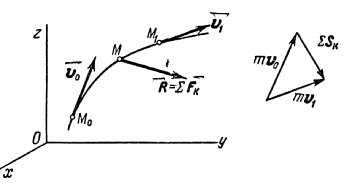
Рис.32

Умножим тогда обе части равенства на dt и возьмем от них определенные интегралы. При этом справа, где интегрирование идет по времени, пределами интегралов будут 0 и t₁, а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорости и . Так как интеграл от d(mv) равен mv, то в результате получим:

Стоящие справа интегралы представляют собою импульсы действующих сил. Поэтому окончательно будем иметь:

Уравнение выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени (рис. 32).

При решении задач вместо векторного уравнения часто пользуются уравнениями в проекциях.

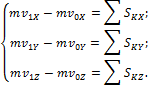
В случае прямолинейного движения, происходящего вдоль оси Ох теорема выражается первым из этих уравнений.

Вопросы для самопроверки

- Что является предметом динамики?

- Сформулируйте основные законы механики.

- Какое уравнение называется основным уравнением динамики?

- Какова мера инертности твердых тел при поступательном движении?

- Зависит ли вес тела от местонахождения тела на Земле?

- Какую систему отсчета называют инерциальной?

- К какому телу приложена сила инерции материальной точки и каковы ее модуль и направление?

- Объясните разницу между понятиями «инертность» и «сила инерции»?

- К каким телам приложена сила инерции, как направлена и по какой формуле может быть рассчитана?

- В чем заключается принцип кинетостатики?

- Каковы модули и направления касательной и нормальной сил инерции материальной точки?

- Что называют массой тела? Назовите единицу измерения массы в системе СИ?

- Что является мерой инертности тела?

- Какая система отсчета называется инерциальной?

- Запишите основной закон динамики в векторной и дифференциальной форме?

- На материальную точку действует постоянная сила. Как движется точка?

- Какое ускорение получит точка, если на нее действует сила, равная удвоенной силе тяжести?

- После столкновения двух материальных точек с массами m₁=6 кг и m₂=24 кг первая точка получила ускорение 1,6 м/с. Чему равно ускорение, полученное второй точкой?

- При каком движении материальной точки равна нулю ее касательная сила инерции и при каком – нормальная?

- По каким формулам вычисляются модули вращательной и центробежной сил инерции точки, принадлежащей твердому телу, вращающемуся вокруг неподвижной оси?

- Как формулируется основной закон динамики точки?

- Приведите формулировку закона независимости действия сил.

- Запишите дифференциальные уравнения движения материальной точки в векторной и координатной форме.

- Выведите дифференциальное уравнение движения свободной материальной точки при трех способах задания движения материальной точки.

- Сформулируйте две основные задачи динамики свободной материальной точки. Посредством каких математических операций они решаются и как именно?

- Что такое начальные условия движения материальной точки и как они записываются при трех способах задания движения?

- Приведите условия, из которых определяются постоянные интегрирования дифференциальных уравнений движения материальной точки.

- Какие уравнения динамики называются естественными уравнениями движения материальной точки?

- Каковы две основные задачи динамики точки, которые решаются с помощью дифференциальных движений материальной точки?

- Дифференциальные уравнения движения свободной материальной точки.

- Сколько постоянных интегрирования войдет в общее решение дифференциальных уравнений движения материальной точки, если она движется в пространстве, на плоскости, вдоль прямой соответственно.

- Как определяются постоянные при интегрировании дифференциальных уравнений движения материальной точки?

- Определение значений произвольных постоянных, появляющихся при интегрировании дифференциальных уравнений движения материальной точки.

- Каковы законы свободного падения тела?

- По каким законам происходят горизонтальное и вертикальное перемещения тела, брошенного под углом к горизонту в пустоте? Какова траектория его движения и при каком угле тело имеет наибольшую дальность полета?

- Как вычислить импульс переменной силы за конечный промежуток времени?

- Что называется количеством движения материальной точки?

- Как выразить элементарную работу силы через элементарный путь точки приложения силы и как – через приращение дуговой координаты этой точки?

- На каких перемещениях работа силы тяжести: а) положительна, б) отрицательна, в) равна нулю?

- Как вычислить мощность силы, приложенной к материальной точке, вращающейся вокруг неподвижной оси с угловой скоростью ?

- Сформулируйте теорему об изменении количества движения материальной точки.

- При каких условиях количество движения материальной точки не изменяется? При каких условиях не изменяется его проекция на некоторую ось?

- Приведите формулировку теоремы об изменении кинетической энергии материальной точки в дифференциальной и конечной форме.

- Что называется моментом количества движения материальной точки относительно: а) центра, б) оси?

- Как формулируется теорема об изменении момента количества движения точки относительно центра и относительно оси?

- При каких условиях момент количества движения точки относительно оси остается неизменным?

- Как определяются моменты количества движения материальной точки относительно центра и относительно оси? Какова зависимость между ними?

- При каком расположении вектора количества движения материальной точки его момент относительно оси равен нулю?

- Почему траектория материальной точки, движущейся под действием центральной силы, лежит в одной плоскости?

- Какое движение точки называется прямолинейным? Запишите дифференциальное уравнение прямолинейного движения материальной точки.

- Запишите дифференциальные уравнения плоского движения материальной точки.

- Какое движение материальной точки описывают дифференциальные уравнения Лагранжа первого рода?

- В каких случаях материальную точку называют несвободной и каковы дифференциальные уравнения движения этой точки?

- Дайте определения стационарных и нестационарных, голономных и неголономных связей.

- Какие связи называют двусторонними? Односторонними?

- В чем сущность принципа освобождаемости от связей?

- Какой вид имеют дифференциальные уравнения движения несвободной материальной точки в форме Лагранжа? Что называют множителем Лагранжа?

- Приведите формулировку динамической теоремы Кориолиса.

- В чем сущность принципа относительности Галилея-Ньютона?

- Назовите движения, при которых кориолисова сила инерции равна нулю.

- Какой модуль и какое направление имеют переносная и кориолисова силы инерции?

- В чем заключается различие между дифференциальными уравнениями относительного и абсолютного движений материальной точки?

- Как определяются переносная и кориолисова силы инерции в различных случаях переносного движения?

- В чем состоит сущность принципа относительности классической механики?

- Какие системы отсчета называются инерциальными?

- Каково условие относительного покоя материальной точки?

- В каких точках земной поверхности сила тяжести имеет наибольшее и наименьшее значения?

- Чем объясняется отклонение падающих тел к востоку?

- В каком направлении отклоняется тело, брошенное вертикально вверх?

- В шахту опускается бадья с ускорением а=4 м/с². Сила тяжести бадьи G=2 кН. Определите силу натяжения каната, поддерживающего бадью?

- На движущийся по прямолинейному горизонтальному пути поезд действует постоянная сила тяги тепловоза, равная силе трения. Какое движение совершает поезд? Как проявляется в этом случае закон инерции?

- Почему нагруженный автомобиль на булыжной мостовой движется более плавно, чем такой же автомобиль без груза?

- На весах уравновешен человек, держащий в руке тяжелый груз. Что произойдет с весами, если человек быстро поднимет груз вверх?

- Какой продолжительности должны быть сутки на Земле, чтобы тела на экваторе не имели веса?

- Почему при прохождении поезда через железнодорожный мост машинист уменьшает скорость поезда.

- Как повлияет на «легкость хода» велосипеда увеличение диаметра его колес? Прочие размеры частей велосипеда считать неизменными.

- Когда Земля быстрее движется по своей орбите вокруг Солнца (для северного полушария) или летом?

- Притяжение Луны Солнцем примерно в два раза больше, чем притяжение ее Землей. Почему же Луна - спутник Земли, а не самостоятельная планета.

- Можно ли так запустить спутник, чтобы он все время находился над одним и тем же пунктом Земли?

- Может ли спутник обращаться устойчиво в плоскости, не проходящей через центр Земли?

- Основные величины системы СИ:

1) метр, килограмм, секунда, Кельвин, моль, канделла, ампер

2) метр, килограмм, секунда

3) метр, килограмм, сила, секунда

4) метр, килограмм, секунда, Кулон

5) сантиметр, грамм, секунда, ампер

- Под массой тела в теоретической механике понимают:

1) вес тела

2) силу притяжения тела

3) инерционность тела

- Понятие силы:

1) отношение массы тела к ускорению

2) физическая причина, влияющая на состояние тела

3) физическая величина, характеризующая изменение формы тела

4) физическая величина, характеризующая изменение скорости тела

5) физическая величина, вектор, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

- Понятие инерциальной системы отсчета:

1) система отсчета, связанная с декартовой системой координат

2) вращающаяся система отсчета

3) система отсчета, движущаяся поступательно

4) система отсчета, в которой справедливы законы Ньютона

5) система отсчета, связанная с Солнцем

- Первый закон Ньютона:

1) сила равна произведению массы тела на ускорение

2) силы, с которыми взаимодействуют два тела, численно равны и противоположны по направлению

3) всякое тело пребывает в состоянии покоя, если сумма сил, действующих на него равна нулю

4) существуют такие системы отсчета, относительно которых всякое тело пребывает в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не изменит этого состояния.

- Второй закон Ньютона в общей форме:

1)

2)

3)

4)

5)

- Основное содержание первого закона Ньютона:

1) свободное тело движется равномерно и прямолинейно

2) тело движется ускоренно, если на него действует внешняя сила

3) постулируется наличие инерциальных систем отсчета

4) определяется явление инерции

5)

- Дайте определение инертности:

1) способность тела сохранять состояние покоя или равномерного и прямолинейного движения

2) обозначает действие одного тела на другое

3) свойство тел оказывать сопротивление попыткам привести его в движение или изменить величину и направление его скорости

4) свойства тела притягивать к себе другие тела

- Как можно сформулировать вторую (основную) задачу динамики для материальной точки?

1) зная закон движения точки определить действующую на нее силу

2) зная действующие на точку силы определить закон движения точки

3) зная закон движения определить реакцию связей, наложенных на точку

- Какое выражение не является основным уравнением динамики поступательного движения

1)

2)

3)

4)

5)

- Две материальные точки движутся по прямой с постоянными скоростями 10 и 100 м/с. Можно ли утверждать, что к этим точкам приложены эквивалентные системы сил?

1) нельзя;

2) можно.

- К двум материальным точкам массой 5 и 15 кг приложены одинаковые силы. Сравните численные значения ускорения этих точек?

1) ускорения одинаковы;

2) ускорение точки массой 15 кг в три раза меньше, чем ускорение точки массой 5 кг.

- Можно ли задачи динамики решать с помощью уравнений равновесия?

1) можно;

2) нельзя.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Строительная механика Сопротивление материалов

Прикладная механика Детали машин Теория машин и механизмов

00:00:00